勒薩吉重力理論
勒薩吉重力理論(英語:)是一種關於重力的動力學理論,最早由尼古拉·法蒂奥·丢勒在1690年提出,隨後又由喬治-路易斯·勒薩吉在1748年重新提出。該理論藉助微小不可見的粒子的流動,對牛頓的萬有引力提出了一種機械解釋[1]。這種微粒勒薩吉稱之為“超凡小體”(),它們會從各個方向撞擊一切物體。根據這種模型,任兩個物體都相互遮蔽了一些撞向它們的小體,因此小體撞擊物體的靜壓力會不平衡,導致兩個物體相互靠近。這種對重力的機械解釋從未得到廣泛認可。
基本理論
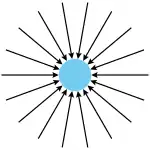
該理論認為,重力是宇宙中的一種微粒(小體)朝各個方向高速運動的結果。理論假定微粒朝各個方向流動的強度完全相同,因此一個孤立物體 A 會被從各個方向以相同的力撞擊,只會有向內的壓力而不會有淨推力(見圖 1)。

但是,如果有第二個物體 B 在場,本來會從 B 的方向撞擊 A 的一小部分粒子就會被攔截,因此 B 就起到了屏蔽的作用,在 B 所在的方向上,A 受到的粒子撞擊會比反方向少一些。類似地,在 A 所在的方向上,B 受到的粒子撞擊也會比反方向少一些。我們可以說 A 和 B 相互“遮蔽”,而這兩個物體會因為撞擊力的不平衡而被推向彼此(見圖 2)。因此,根據勒薩吉的理論,這種物體之間的表象上的吸引力,實際上是因為從另一物體的方向而來的推力減小。故而這種理論有時被稱為「推力重力」(push gravity)或者「遮蔽重力」(shadow gravity),雖然它更常被叫做「勒薩吉重力」(Le Sage Gravity)。
碰撞的本性

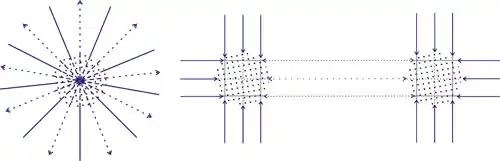
如果物體 A 和重力微粒的撞擊是完全彈性碰撞,則從物體反射的微粒強度將會和入射微粒相同,因此不可能會有淨推力。但是,這件事即使在引入第二個物體 B 時也會是對的。雖然 B 起到了屏蔽的作用,使本來會撞向 A 的重力微粒被 B 擋住,但是會有別的本來不會撞上 A 的粒子,在經過撞擊 B 改變方向後,替代那些本來應該撞向 A 的粒子。因此如果這種碰撞是完全彈性的,那麼在 A 和 B 之間反射的粒子就會完全補償遮蔽作用。所以,如果要產生淨重力,就必須要假設這種碰撞不是完全彈性的,或至少有一部分反射回來的粒子變慢了,它們的動量將比撞擊前少。如此一來,對單個物體 A,會有一些粒子以減弱的動量離開 A,另一些粒子以未減弱的動量抵達 A,最終會產生一個指向 A 物體中心的淨動量(見圖 3)。在這種假設中,兩個物體間反射的粒子就不會完全補償遮蔽作用,因為反射流比入射流會弱一些。
平方反比定律
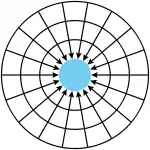
由於我們假設撞擊在物體上的一些(或全部)重力微粒被該物體吸收(或減慢),因此從物體處散發出去的重力微粒的通量強度,將小於指向該物體的重力微粒。我們可以想像這種動量流的不平衡,及由此產生的施加在附近其他物體上的力的不平衡,會均勻分佈在以物體為中心的球形表面上(見圖 4)。在包圍物體的球形表面上,動量流不平衡的程度與包圍球的大小無關,而球形的表面積則按半徑的平方成比例增加。因此,每單位面積上的動量不平衡,會與距離的平方成反比。
與質量成正比
從目前概述了的幾個前提來看,重力微粒只能產生與物體表面積成比例的力。但是引力卻應該與質量成正比。為了滿足與質量成正比的需求,勒薩吉理論認為:一)物質的基本元素很小,因此整個物體主要由空白空間組成; 二)重力微粒非常微小,因此只有很小一部分會被物質攔截。因此,每個物體內部的“遮蔽部分”與物質的每個基本元素的表面積成正比。如果接著假設物質不可穿透的基本元素都是相同的(即密度與表面積的比率相同),那麼遮蔽效果就會(至少是近似)與質量成正比(圖 5)。
法蒂奧
尼古拉·法蒂奧在其 1690 年春天寫給克里斯蒂安·惠更斯的信中,第一次對他的重力理論做出表述。[2]兩天後,法蒂奧在倫敦皇家學會宣讀了這封信的內容。在接下來的幾年中,法蒂奧撰寫了他的主要著作《論重力的成因》(De la Cause de la Pesanteur)的幾段手稿,但這些材料在他生前沒有出版過。1731 年,法蒂奧還以盧克萊修的風格把他的理論譜寫成拉丁語詩作寄給了巴黎科學院,但被退稿了。前述手稿的一些片段,以及這首詩的副本,後來被勒薩吉得到,但他未能找到願意出版法蒂奧論文的出版商。[3]直到 1929 年,卡爾·博普(Karl Bopp)才出版了法蒂奧手稿的唯一完整複本[4],而到了 1949 年,加涅賓(Gagnebin)才使用勒薩吉收集的片段來重建論文[5]。加涅賓版包含了法蒂奧在 1743 年以前做的全部修訂,這距他撰寫博普那份複本所依據的草稿已有 40 年了。但是,博普版的後半部分包含法蒂奧理論中數學上最先進的部分,但加涅賓並未將其包括在內。有關法蒂奧作品的詳細分析,以及博普版和加涅賓版副本之間的比較,請參見 Zehe 的著作[6]。以下描述主要基於博普版。
法蒂奧的金字塔(問題 I)

法蒂奧假設宇宙中充滿了微小的粒子,這些粒子以極高的速度在各個方向上直線移動。為了描述他的想法,他使用了下面一個例子:假設有個物體 C,在其上畫出無限小的平面 zz,和以 zz 為中心的球體。 法蒂奧在此球體中放置了金字塔 PzzQ,其中一些粒子沿 zz 方向流過,還有一些粒子已經被 C 反射,並因此離開 zz。 法蒂奧認為反射粒子的平均速度比入射粒子低,因此其動量也較弱,故會產生某種流,將所有物體推向 zz 方向。一方面,流的速度保持恆定,但另一方面,與 zz 的距離越近,流的密度就越高,因此其強度與 1/r2 成正比。由於可以在 C 周圍繪製無限數量的這種金字塔,因此這一比例適用於 C 附近的整個範圍。
微粒速度的減少
為表明粒子在反射後行進速度會減小的假設合理,法蒂奧進一步陳述了以下假設:
陳述這些假設的段落是法蒂奧理論中最費解的部分,因為他沒有清晰表明他覺得哪一種碰撞方式更合理。但是,在他理論 1742 年的新版中,他縮短了相關的段落,將“完全彈性或彈力”歸給顆粒,另一方面將“不完全彈性”歸給物體。依此,微粒會以減弱的速度反射。法蒂奧還面臨另一個問題:如果這些微粒互相碰撞會發生什麼事?非彈性碰撞將導致粒子速度穩定下降,從而導致重力降低。為了避免該問題,法蒂奧假定粒子的直徑與其相互間的距離相比非常的小。
微粒的凝聚
法蒂奧長期以來一直認為,由於這些微粒接近物體的速度高於(反射之後)遠離物體的速度,微粒會在物體附近不斷積累(他稱這種現象為“凝聚”)。但是,他後來意識到,儘管進入的微粒更快,但它們之間的間隔也會比反射的微粒更遠,因此向內和向外的總粒子流相等。因此,微粒的長期積累不存在,反射微粒的密度保持恆定(假設這些微粒足夠小,在物體附近不會發生明顯的相互碰撞)。更重要的推論是,法蒂奧指出,通過同時增加微粒的速度和彈性,可以任意減小入射和反射微粒的速度(以及密度)之間的差異,同時仍保持相同的等效重力。
物體的空隙

為確保這種重力會和質量成正比,法蒂奧假設微粒流動對物體的穿透性非常高。他簡述了三種模型來表達該假設是對的:
- 他認為一切物體都是某種“小球”的積聚物,這些“球”的直徑與它們彼此之間的距離相比“無限”小。但是他拒絕了這一提議,因為在這種情況下,物體之間會互相接近,不會保持穩定。
- 他又假設這些球可以通過桿或線連接起來,並會形成某種晶體結構。但是,他也拒絕了該模型——如果多個小球在一起,那麼重力微粒的流體將無法在所有方向上均等地穿透該結構,因此重力不可能與質量成正比。
- 最後,法蒂奧把這些球去掉,只留下了桿或者說它們組成的網格。通過使它們“無限地”小於它們彼此之間的距離,就能實現最大的可穿透性。
微粒的壓力(問題 II)
在 1690 年法蒂奧就假定,微粒在平面上施加的“推力”是這種重力理論的第六部分,如果所有粒子都垂直於平面就會產生這種推力。法蒂奧通過計算該力的大小來證明自己的推測。該力被施加在某個點 zz 上。他推導出如下公式:p = ρv2zz/6。這個解和氣體動力論中為人熟知的公式 p = ρv2/3 非常像,而後者是由丹尼爾·伯努利在 1738 年提出的。這是第一次有人指出一種和氣體動力論可相類比的解——遠在後者理論中的基本概念發展之前。 但是,伯努利的壓力值比法蒂奧大兩倍。根據 Zehe 的研究,這是因為法蒂奧將碰撞後的動量變化計算成 mv 而非 2mv,因此得到了錯誤結論,他的結果只對完全非彈性碰撞正確。 法蒂奧不只試圖將這種解用來解釋重力,還想用於解釋氣體的行為。他試圖構造一個溫度計,能指出空氣分子的“運動狀態”,從而可以估算溫度。但是法蒂奧(與伯努利不同)沒有發現熱和空氣的運動是“相同”的——他用另一種流體來解釋空氣分子的運動。伯努利是否受到法蒂奧的影響是未知的。
無限(問題 III)
在這一章中,法蒂奧研究了“無限”這一術語與其理論之間的關係。 法蒂奧經常以某些現象比其他現象“無限小或無限大”的事實來證明他的想法是正確的,在這種情況下,很多問題就可以減小到無法探測可以忽略的值。例如,晶體結構中桿的直徑無限小於彼此之間的距離,或粒子的速度比物體的速度無限大,或反射和非反射粒子之間的速度差無限小。
介質的阻力(問題 IV)
這是法蒂奧的理論中,在數學上最複雜的部分。在這一章他試圖估計微粒流對移動中的物體產生的阻力。假定 u 是物體的速度,而 v 是重力微粒的速度,ρ 是微粒介質的濃度。在 v ≪ u 並且 ρ 是一個常數的情況下,法蒂奧計算出阻力為 ρu2。在 v ≫ u 且 ρ 是一個常數的情況下,阻力則是 4/3ρuv。牛頓指出天體的軌道運動不應受到這種阻力影響,這要求空間中的任何介質都必須非常稀疏。因此法蒂奧減小了微粒的密度,並指出為了維持足夠的重力,粒子密度的減小應該要由“依密度的平方反比”增加 v 來補償。這是從法蒂奧的粒子壓力理論得到的,這一壓力正比於 ρv2。根據 Zehe 的研究,法蒂奧只要試圖把 v 增大到非常高的值,實際上就能夠使這種阻力(相對於重力而言)非常小,因為在法蒂奧的模型裡,阻力在此時正比於 ρuv 但是重力(即微粒帶來的壓力)正比於 ρv2。
法蒂奧理論的反響
法蒂奧曾和與他同一時代的最著名的科學家之間進行過交流。
在1690年至1693年之間,艾薩克·牛頓與法蒂奧之間有牢固的個人關係。牛頓對法蒂奧理論的陳述差異很大。例如,1962 年,在牛頓自己持有的《原理》(Principia)印刷複本中,他在描述了對重力的機械解釋的必要條件以後,寫下了一段(未出版的)註解:“然而唯一可以解釋重力的[機械]假設就是這種假設,而這種解釋則由最靈巧的幾何學家 N. Fatio 先生首次設計出來”[6]。另一方面,法蒂奧本人則表示,儘管牛頓私下評論說法蒂奧的理論是對其引力最好的機械解釋,他自己清楚牛頓傾向於相信引力的真正解釋不是機械的。另外,數學家格里高利在他的《備忘錄》(Memoranda)中指出:“牛頓先生和哈雷先生嘲笑法蒂奧先生解釋重力的方式。” [6]據稱,這是他在 1691 年 12 月 28 日注意到的。但是,他實際寫下這段話的日期卻是未知的,因為使用的墨水和羽毛都與頁面的其餘部分不同。1694 年後,牛頓與法蒂奧兩人的關係逐漸淡化。
克里斯蒂安·惠更斯是最早獲知法蒂奧理論的人,但他從未接受。法蒂奧相信他已經說服了惠更斯其理論是一致的,但是惠更斯在給哥特佛萊德·萊布尼茲的信中否認了這一點。法蒂奧和萊布尼茲之間在理論上也有短暫的往來。萊布尼茲出於哲學理由拒絕在微粒間留出空隙,因此批評了法蒂奧的理論。 雅各布·伯努利對法蒂奧的理論表示有興趣,並敦促法蒂奧用完整的手稿來寫他的引力思想,而法蒂奧實際寫了一份。伯努利複製了該手稿,現在存於巴塞爾大學圖書館中,並且是前述的博普版複本的基礎。
雖然法蒂奧和這些科學家都有交流,除了克拉默和勒薩吉等,其理論仍然不為人知。這是因為法蒂奧從未能夠正式出版自己的作品,而且他受到了一群宗教狂熱分子的影響,他們被人稱作“法國先知”(屬於卡米撒派),這使得他的公眾聲譽遭受破壞。
克拉默與雷德克
1731 年,瑞士數學家加布里爾·克拉默(Gabriel Cramer)發表了一篇論文,[7] 末尾出現了與法蒂奧理論非常相似的理論綱要——包括物質的網狀結構,重力和光的類比,以及遮蔽作用——但沒有提及法蒂奧的名字。 法蒂奧知道克拉默能夠得到他主要論文的副本,因此指責克拉默只是重複他的理論且沒能夠讀懂。不過,勒薩吉同樣是經克拉默告知,才在 1749 年知道法蒂奧的理論。1736 年,德國醫生弗朗茲·阿爾伯特·雷德克(Franz Albert Redeker)也發表了類似的理論。[8]尚未知曉雷德克和法蒂奧之間存在的任何關係。
勒薩吉

勒薩吉第一次闡述自己的理論,是在 1748 年,他將自己的論文《論死力的起源》(Essai sur l'origine des forces mortes)[9]提交予位於巴黎的法國科學院,但該論文從未被出版。[3]根據勒薩吉自己的說法,是在他寫出並發表這份論文之後,他才知道法蒂奧、克拉默和雷德克的理論。勒薩吉的理論闡述第一次出版,則是在 1756 年,[10]。1758 年,在他參與位於盧昂(Rouen)的法國科學院舉辦的競賽時,提交了一篇更細緻的論文,《論化學力學》(Essai de Chymie Méchanique)[11] 。在這篇文章中他試圖同時解釋重力和化學親和力的本性。公眾獲知該理論,則要到 1784 年,他出版《牛頓式的盧克萊修》(Lucrèce Newtonien),在該文中他將他理論和盧克萊修觀念的對應關係發展成熟。[12] 另一篇關於其理論的闡述,則是在他死後,由皮耶爾·普瑞弗斯特在 1818 年出版。[13]
勒薩吉的基本概念

勒薩吉非常詳細地討論了自己的理論,並且提供了對理論部份參數所做的定量估計。
- 他把重力微粒叫做超凡小體,因為他假定這些小體來自我們已知的宇宙之外。超凡小體的流動分佈是各向同性的,而其傳播的規律則和光非常相似。
- 勒薩吉認為如果一般物體和微粒的碰撞是完全彈性的,就不會有任何重力。因此他假定這些微粒和物體的基本組成成份是“絕對堅硬”的,並斷言由此可以得出相當複雜的相互作用形式——如果微粒從垂直於一般物體表面的方向碰撞,那就是完全非彈性的,如果從其表面的切線方向碰撞,就是完全彈性的。他隨後評註這蘊含了散射微粒的平均速度會是入射微粒的 2/3。為了避免微粒之間的非彈性碰撞,他假定微粒的直徑相對於它們之間的距離非常小。
- 微粒流帶來的阻力正比於 uv(v是微粒的速度而u是物體的速度),而引力則正比於v2,因此只要提高v的值,阻力和重力之比就可以任意地小。因此,他認為“超凡小體”可能以光速運動。但在進一步考量後,他又把這個數值調整為光速的 105 倍。
- 為保證重力和質量成正比,推斷一般物體由籠狀結構組成,其節點直徑只有它們相互距離的 107 分之一,而組成籠狀結構的“桿”相對於籠狀結構本身也非常小(其長度是厚度的 1020 倍),因此微粒可以在幾乎沒有被阻攔的情況下穿過物體。
- 勒薩吉也試圖用遮蔽機制來解釋凝聚力的存在,以及不同強度的其他力,他假定超凡小體有多種類型,彼此尺寸不同,如圖 9 所示。
勒薩吉宣稱他是第一個得出這種理論所有結論的人,普瑞弗斯特也認為勒薩吉的理論比法蒂奧的理論更成熟。[3] 但是,在對法蒂奧的論文(勒薩吉也擁有這些論文)進行細緻分析之後,Zehe 比較了兩人的理論,判斷勒薩吉沒有做出實質上的新貢獻,而且他常常沒有達到法蒂奧的推論深度。[6]
勒薩吉理論的反響
勒薩吉的觀念在他的時代並沒有獲得正面評價,除了他的少數朋友和同僚,例如皮耶尔·普瑞弗斯特,夏勒·博內(Charles Bonnet),尚-安德烈·德呂克(Jean-André Deluc),查爾斯·斯坦厄普(Charles Mahon, 3rd Earl Stanhope),以及賽門·留利爾(Simon Lhuilier)。他們在他們的著作和論文中提及並描述了勒薩吉的理論,曾為他們的同代人用作理解勒薩吉理論的二手信源(因為勒薩吉本人出版的論文甚少)。
歐拉、伯努利與博什科維奇
李昂哈德·歐拉在 1761 年曾經評論勒薩吉的理論比其他作者的理論都來得“無限地好”,而所有反駁都被這一模型抵消,但接下來就說該理論和光的類比對他而言毫無重量,因為他相信光的本性是波動。在進一步考量下,歐拉基本拒絕了該理論,並在 1765 年寫信給勒薩吉說:[14]
| 先生,請原諒我,如果我對您超凡小體的理論感到非常不耐,因為我總是更偏好坦承我對重力成因的無知,而不是訴諸這些奇怪的假設。 |
丹尼爾·伯努利樂於見到勒薩吉理論與其對氣體本性的想法間的相似性。但是,伯努利認為自己的氣體動力論只不過是一種推測,因此類似地也認為勒薩吉的理論是高度推測性的。[15]
羅傑·約瑟夫·博什科維奇(Roger Joseph Boscovich)指出,勒薩吉理論是第一個能實際用機械過程解釋重力的理論。但是他拒絕了這個模型,因為模型中有大量未使用的超凡小體。約翰·普萊費爾(John Playfair)如此描述博什科維奇的論證:
| 巨量的粒子,因此註定在無窮空間中繼續他們永不完結的旅程,既不改變方向,也不回到它們的來處,這種假設幾乎不為自然通常的儉省所支持。這無數洪流的動力從何而來?肯定是需要某種創造性力量的永恆努力,而這種力量又得在幅度和持續時間上無窮無盡吧?[16] |
馬克士威後來提出了一個非常相似的論證(見下方小節)。另外,博什科維奇完全拒絕用接觸力和瞬間推動力來解釋重力,他認為引力是一種超距作用。
利希滕貝格、康德與謝林
格奧爾格·克里斯托夫·利希滕貝格關於勒薩吉理論的知識[17]是依靠《牛頓式的盧克萊修》和普瑞弗斯特的一篇綜述得來。利希滕貝格最早(像笛卡爾那樣)相信自然現象的所有解釋都必須要從直線運動和推動力而來,而勒薩吉的理論滿足了這些條件。在 1790 年,他在一篇論文中表達對這一理論的熱忱,相信勒薩吉的理論已懷有一切已知知識,使得在重力主題上的進一步幻想全無用處。他接著說:“如果這是一場夢,那麼它是人所做過的最偉大而又雄壯的一場夢,我們能填上我們書卷中的漏洞,而這漏洞只能用夢來補上”。[18]
他在哥廷根大學的物理學講座上經常援引勒薩吉理論。然而,在 1796 年利希滕貝格被伊曼努爾·康德的論證說服,因而改變了觀點。康德批評了一切試圖用推動力取代吸引力的理論。[19]康德指出,物質在空間上延展的一切構造,例如半徑不為零的微粒,如果要存在,都必然要有某種結合力把其延展的各部分凝聚起來。這種力無法用重力微粒的推力來解釋,因為這些微粒也必須以同樣形式凝聚。為了避免這種循環論證,康德斷定一定存在某種基本的吸引力。這種駁斥正是一世紀前對笛卡爾推動力學說的駁斥,而它甚至讓笛卡爾的追隨者都放棄其哲學理論的這一方面。
拉普拉斯
皮耶-西蒙·拉普拉斯試圖得到合乎天文觀察的引力的速度時,部分參考了勒薩吉的理論。他計算出其速度必須“至少是光速的一億倍”,才能夠避免重力傳播延遲使觀測到的月球軌道有太大的畸變。[21]包括拉普拉斯在內的多數研究者都以此支持牛頓的超距瞬時作用觀念,並且認為任何類似勒薩吉理論的模型都不可信。拉普拉斯同時論證要維持重力和質量成正比,地球的分子表面積最多是其可見表面積的千萬分之一。拉普拉斯從未在其成果中直接提及勒薩吉的理論,這讓勒薩吉很失望。
動力論
因法蒂奧,克拉默與雷德克的理論都不甚為人所知,在 19 世紀下半葉,隨氣體動力論的發展,勒薩吉的闡述使得對該理論的興趣重燃。
勒雷
為了產生淨重力,勒薩吉的微粒必定在與一般物體碰撞時失去速度,因此會有大量能量轉換成內能。如果微粒的運動模式不存儲內能,則這些能量只能由一般物體所吸收。對該問題,讓·勒雷(Armand Jean Leray)[22]提出了一種微粒模型(與勒薩吉的模型十分相似),斷定吸收來的能量被物體用於產生磁性和熱。他認為這可能是星辰向外發散的能量的來源。
開爾文與泰特

勒薩吉自己的理論在十九世紀下半葉成為重燃興趣的主題,是因為開爾文在 1873 年出版的論文。[23]和勒雷不同,他精確地處理了熱的問題,並認為吸收來的能量將會極高,能在幾分之一秒內就蒸發一切物體。因此,開爾文重複了法蒂奧曾在 1690 年代提出的觀念,來試圖解決勒薩吉理論固有的熱力學問題。他認為這些過量的熱必須被微粒本身吸收,並推測重力物質有渦旋的本性。換言之,微粒原先平移產生的動能必須轉化成不同的運動模式(主要是振動和轉動)來存儲內能。藉助魯道夫·克勞修斯的推論——氣體分子在任何特定運動模式下的能量與其總能量的比值趨於固定——開爾文接著認為因此蓄能但運動速度更慢的微粒會由於(在宇宙學尺度上)跟其他微粒的碰撞回復原先的運動狀態。開爾文還斷言可以從超凡小體流中汲取無窮的自由能,並描述了一個可以做到這點的永動機。
隨後,彼得·格斯利·泰特認為勒薩吉理論是當時已提出的所有重力解釋中唯一可信者。他接著說:
| 該理論最奇特之處在於,假使它是真的,我們有可能推導出一切種類能量最終都是動能。[24] |
開爾文自己對勒薩吉理論最終能得到對現象的完整描述一事並不樂觀。在前述的 1873 年出版的扼要的論文後,他再也沒有重返這個主題,除了下述的一段評論[25]:
| 這種物質的動力學理論只是一個夢,除非它能解釋化學親和力、電、磁、重力、以及聚集渦旋的慣性。勒薩吉的理論可能給我們對重力的解釋,及其在原子渦理論下,與物體慣性的關係——如果這不是來自晶體結構必然有的各向異性,加上重力似乎完美的各向同性的話。但沒有任何已被發現的、或者可以想象的路標指出可能翻越這種困難、或者可能扭轉其缺陷的道路。[26] |
普雷斯頓
薩繆爾·托爾弗·普雷斯頓(Samuel Tolver Preston)[27] 闡明勒薩吉對重力微粒做的許多假設(例如直線運動,極少相互碰撞,等等)可以被統一在同一個觀念下,即它們(在宇宙學尺度上)類似擁有極長平均自由徑的氣體分子。普雷斯頓也接受了開爾文對微粒具有的儲存內能的運動模式的假定。他用如下的例子說明開爾文的模型:用一個鋼鐵環與鐵砧碰撞時,鐵砧不會有太大的震動,但是鋼環卻會振動,並以衰減的速度離開。他同時認為,微粒的平均自由徑至少是行星之間的距離——在更長的距離上,粒子就會由於碰撞重新得到其平移能量,因此他下結論在這麼長的距離上物體之間不會有吸引力,和微粒的大小無關。
保羅·德汝德(Paul Drude)認為這可能可以和卡爾·諾依曼(Carl Gottfried Neumann)與胡戈·馮·澤利格(Hugo von Seeliger)兩人的理論鏈接,他們假定重力在開放空間中會在某種意義上被吸收。[28]
馬克士威

詹姆斯·克拉克·馬克士威於 1875 年,在第九版《大英百科全書》的〈原子〉條目下綜述了開爾文—勒薩吉理論[29]。在描述該理論的基本概念後他寫道(據 Aronson 所言,是種諷刺[30]):
| 此處所呈現的似乎就是一條通向解釋重力律則的道路,若能證明它在其他方面與事實一致,那它也許就會成為通往科學奧秘的皇家之路。[29] |
馬克士威評論了開爾文對微粒有不同能量模式的見解,認為這蘊含重力微粒並不是簡單的原始物質,而是一種有結構的系統,它自己內部仍有儲存內能的運動模式,而這結構必須要由(未被解釋的)吸引力來維持。他認為物體的溫度,即物體分子的平均動能,必然趨近於超凡小體的平均動能,因此,由於後者遠遠大於前者,他作結認定普通物體應該在勒薩吉微粒的轟炸下,在幾秒鐘內焚燒殆盡。[29] 他寫道:
| 我們為該理論投入的空間似乎比它應得的更多,這是因為它很巧妙,並且因為它是迄今為止對引力起源的唯一一種可以被攻擊和捍衛的理論。[29] |
馬克士威還認為,該理論要求“消耗大量外力”,因此違反了作為自然基本原理的能量守恆。[29] 普雷斯頓對馬克士威的批評作出了回應,他認為如果微粒的質量足夠小(並且數量密度足夠大),就可以任意降低每個單個簡單顆粒的動能。但是後來龐加萊對這個問題進行了更詳細的討論,他表明勒薩吉模型中的熱力學問題仍然沒有解決。
艾森卡赫、李沙尼克和杜博依斯-雷蒙
卡斯帕·艾森卡赫(Caspar Isenkrahe)於 1879 到 1915 年間在多份出版物中描述自己的模型。[31]他的基本預設非常接近勒薩吉和普雷斯頓,但他更加詳細描述了這種動力學的應用。但是,斷言小體在碰撞後的速度減少卻沒有任何物體的能量上升,這讓他的模型違反能量守恆定律。他注意到物體的重量和密度之間有關聯(因為如果物體密度下降,那麼物體內部的重力遮蔽就會減少),因此他斷定溫熱的物體應該比冷的物體更重(和熱脹冷縮效應相關)。
1887 年,阿達伯特·李沙尼克(Adalbert Ryšánek)的另一個模型[32]也做了仔細的分析,並運用了麥克斯韋的氣體速度分佈律。他還區分開重力介質和以太。這是有必要的,因為根據他的計算,如果重力介質同時是光行進的介質,則海王星軌道沒有拖曳效應(即受到微粒介質的阻力)意味著微粒速度最少要是 5 · 1019 cm/s。他(類似勒雷)認為吸收的能量會轉化成熱,而這些熱可能轉移入以太,或者供恆星維持能量放出。但是,這些定性推論並沒有被任何關於實際產熱量的定量估計支持。
1888 年,保羅·杜博依斯-雷蒙(Paul du Bois-Reymond)駁斥勒薩吉的理論,部分由於勒薩吉理論預測的重力並非嚴格與質量成正比。為像在牛頓理論中那樣得到精確的質量正比律(這意味著沒有遮蔽或飽和作用,而物質的結構多孔且無限稀疏),超凡小體流必須無限強。杜博伊斯-雷蒙認為這很荒謬。另外,他像康德一樣注意到勒薩吉理論無法達成其目標,因為他使用“彈性”或者“絕對堅硬”等概念,而這(在他看來)只能由超距吸引力解釋。同樣的問題也發生在對分子的結合力的解釋上。因此,他認為這種理論的根本意圖,即拋棄掉作為超距吸引力的基本力,是無法達到的。[33]
波模型
凱勒與德布瓦博德蘭
1863 年,法蘭索瓦·安東尼·愛德華·凱勒(François Antoine Edouard Keller)與 Em. 凱勒(Em. Keller)[34]提出把勒薩吉式力學和以太縱波結合在一起的理論。他們假設這些波在各個方向傳播,並且當撞擊物體時就減少一些動量,因此波在物體間造成的壓力就會比在物體周圍造成的壓力來得小。1869 年,保羅·埃米爾·勒科克·德布瓦博德蘭(Paul-Emile Lecoq de Boisbaudran)[35]提出和勒雷相同的理論(包括熱的生產和吸收),但類似凱勒氏,他也把微粒換成以太縱波。
勞侖茲
在上述嘗試後,二十世紀早期的其他作者也試圖把勒薩吉的微粒替換成電磁輻射。這和當時的勞侖茲以太理論(Lorentz ether theory)和電子理論相關,它們假定物質有帶電的結構。
1900 年,亨德里克·勞侖茲[36]認為勒薩吉的微粒模型和當時的電子理論不兼容。但後來發現電磁波列可以產生一些壓力,而且倫琴射線(現在稱為X射線)具有強大的穿透力,讓他認定沒有什麼可以反對可能存在比X射線更有穿透力的輻射,這種輻射可以替代勒薩吉的微粒。勞侖茲證明帶電粒子之間的吸引力確實可能存在(這種帶電粒子可能用於物質基本亞單元的模型),但只有在入射能量完全被吸收的時候才會發生。該問題也是微粒模型面對的基本問題,因此勞侖茲寫道:
| 然而,情況是這樣:這種吸引力只有在電磁能量以某種方式不斷消失的情況下才可能存在,這種情況極為難見,以至於已述的不能說解釋了引力。這也不是唯一可以提出的反對意見。如果萬有引力的機制是以光速行進的穿越以太的振動,那麼與天文學觀測容許的程度相比,引力應該會對天體運動產生更大的影響。 |
1922 年[37] ,勞侖茲首先檢視了馬丁·克努森(Martin Knudsen)的稀有氣體研究,並將此與他對勒薩吉微粒模型的討論聯結在一起,隨後總結了他自己的電磁勒薩吉模型——但他重複了他 1900 年的結論:沒有吸收就沒有重力效應。
在 1913 年大衛·希爾伯特援引並批評了勞侖茲的理論。他論證如果兩個原子的距離相對重力電磁波長而言足夠大,就不可能有形如 1/r2 的力產生。[38]
約瑟夫·湯姆森
1904 年,約瑟夫·湯姆森[39]也考慮了一種勒薩吉式的模型,其中原始的超凡流是以一種假設性的、比X射線更有穿透力的輻射形式存在。他認為馬克士威的熱問題可以避免,只要假定吸收來的能量不是轉化成熱,而是重新輻射出依然具備高穿透性的輻射流。他注意到這個過程可能可以解釋放射性物質的能量從何而來——然而,他也表明放射性的來源更可能是物質內部。1911 年湯姆森在大英百科全書第十一版中名為“物質”的條目[40] 下回到該主題。他在該文說,這種二次輻射的形式有點類似於帶電粒子穿過物質的過程如何引起甚至更具有穿透的X射線的輻射。他說:
| 最近發現的一個非常有趣的結果是,勒薩吉為其理論目的引入的機械過程,與我們現在有直接的實驗證據驗證的事物非常相似。……然而,就我們所知,倫琴射線在被吸收時並沒有產生更具穿透力的倫琴射線——要用它們解釋吸引力,這應該要發生——但會產生穿透力較小的射線或同類的射線。[40] |
晚近評估
達爾文
1905年,喬治·達爾文(George Darwin)計算了兩個物體在非常近距離時,其間的重力,以確定幾何效應是否會導致牛頓定律被違反。[43] 在這裡,達爾文用尺寸均一的微觀硬球體代替了勒薩奇的籠狀物質結構。他的結論是只有在完全非彈性碰撞(零反射)的情況下,牛頓定律才會嚴格成立,這加強了勒薩吉理論的熱力學問題。同樣,只有在衝擊的法向分量和切向分量都完全無彈性(與勒薩吉的散射機制相反)且物質基本粒子的大小完全相同時,這種理論才有效。他接著推論,輻射光的物體之間的推力,和完全吸收勒薩吉微粒造成的效果是可相互類比的。而表面溫度不同的物體的各個部份將朝著較冷的部分移動。在後來對引力理論的綜述中,達爾文簡要描述了勒薩吉的理論,並說他認真考慮了該理論,但隨後寫道:
| 我不會進一步提及這個概念,只能說我相信沒有任何科學人願意承認它提供了真正的道路。[44] |
龐加萊
部分基於達爾文的計算,亨利·龐加萊在 1908 年對勒薩吉理論提出了重要的批評。[45]他認定理論產生的吸引力正比於, 其中 S 是地球表面的分子的總面積,v 是重力微粒的速度,ρ 是微粒介質的密度。與拉普拉斯一樣,他論證要維持重力和質量成正比,S 最多只能是地球可見表面積的千萬分之一。而微粒帶來的拖曳效應(即微粒介質帶來的阻力)正比於 Sρv,因此拖曳效應與引力的比反比於Sv。要減小拖曳效應,龐加萊認為 v 最少必須是光速的 24 · 1017 倍。現在有了 Sv 和 v 的最小容許值,和 S 的最大容許值,就可以算出產生的熱,它正比於 Sρv3。該計算表明地球的溫度將每秒上升 1026 度。龐加萊因此注意到“地球不能長期忍受這樣的轄制”。龐加萊也分析了一些波模型(托馬西納與勞侖茲的),認為它們和微粒模型有同樣的問題。為減少拖曳效應,波的速度同樣必須超光速,也同樣會有熱問題。在描述和湯姆森類似的再輻射模型後,他下結論道:“這就是我們試圖使勒薩奇的理論站得住腳時,被引導著做出的複雜假設。”
他還指出,如果在勞侖茲模型中將吸收的能量完全轉換為熱量,則每秒將使地球溫度升高 1013 度。龐加萊接著在 19 世紀末和 20 世紀初發展出的“新動力學”的背景下繼續研究勒薩吉的理論,特別考慮到了相對論原理。對於微粒理論,他指出“很難想像與相對性原理相容的碰撞定律”,並且仍然存在阻力和發熱問題。
預測與批評
物質的稀疏性
該理論的基本預測是物質會極端稀疏。正如法蒂奧和勒薩吉在 1690/1758 年(以及之前的惠更斯)所假設的那樣,物質的主要組成必須是空白空間,這樣微粒才能幾乎不受干擾地穿透物體,使物體的每一部分都可以參與引力相互作用。一段時間後,該預測(在某些方面上)獲得證實。物質的確主要由空白空間組成,某些粒子(如中微子)幾乎可以不受阻礙地穿過物質。但是,基本粒子作為古典實體的圖景——靠直接碰撞來進行相互作用,而其作用情況取決於它們的形狀和大小(例如法蒂奧/勒薩吉提出的網格結構以及艾森卡赫/達爾文的均一球體)——與當前對基本粒子的理解不一致。勞侖茲/湯姆森將帶電粒子作為物質基本成分的建議也與當前的物理學相矛盾。
宇宙輻射
每個勒薩吉式的模型都假設存在一個具有巨大強度和穿透力的、充滿空間的各向同性微粒流或輻射。這與 20 世紀發現的宇宙微波背景輻射(CMBR)有一些相似之處。 CMBR 確實是一個充滿空間且各向同性的輻射流,但是它的強度和穿透能力都非常小。來自(例如)太陽的中微子流具有勒薩吉為其超平凡小體所設想的穿透性,但這種粒子流卻又不是各向同性的(因為個別恆星是中微子的主要來源),強度甚至更低於 CMBR。當然,CMBR 和中微子都不會以超光速傳播,但這卻是勒薩吉粒子的另一個必要屬性。理察·費曼曾從更現代的角度來考慮,摒棄勒薩吉簡單的“推力”概念,中微子(或其他類似中微子的粒子)也許可能是引力的量子場論中的中介粒子,但隨後該想法又被他自己駁斥。[46]
重力遮蔽

儘管在法蒂奧—勒薩吉理論中一般假設物質非常稀疏,但物質不會完全可被穿透,否則就不存在引力。但是,這會帶來問題:如果物體的質量足夠大,兩塊物體產生的陰影量,將由於陰影重疊,而少於它們各自陰影產生的陰影總和(圖 10,上半)。這種稱為重力屏蔽的假想效果意味著在添加物體時,重力的增幅不會與質量成正比。因此,為了保持理論設想可行,法蒂奧和勒薩吉都假設屏蔽效果小到無法被檢測,換言之,要求物質相互作用的截面必須非常小(圖 10,下半)。但為了要得到我們實際觀測到的重力大小,這意味著引力流的最小強度也必須非常高。任何形式的引力屏蔽都將違反等效原理,並且與厄缶實驗(Eötvös experiment)及其後續實驗中觀察到的極其精確的零結果(null result)不一致——所有這些結果都證實了廣義相對論的預測,即主動引力質量、被動引力質量和慣性質量完全相等。[47]有關引力屏蔽與勒薩吉引力之間關係的更多歷史信息,請參閱 Martins 的文章[48][49]和 Borzeszkowski 等人的文章[50]。
由於艾森卡赫關於密度、溫度和重量之間關係的論斷完全基於預測材料密度變化產生的影響,並且同一密度的物體可以升溫也可以降溫,因此艾森卡赫的評論並不能推導出溫度和重力之間的任何基本關係。(實際上,溫度和引力之間、原子結合能和引力之間確實存在關係,但是它們的實際效應與艾森卡赫的推測無關。請參見下面的“結合能”一小節。)至於對引力和物體密度有關的預測,所有實驗證據都指示不存在這種關係。
拖曳效應
根據勒薩吉的理論,如果孤立的物體相對於超凡小體流的各向同性參考系(即在各個方向上超凡微粒的速度均相同的參考系)運動,則它會受到拖曳阻力的作用。這是由於以下事實:如果物體處於運動狀態,則從前面撞擊物體的微粒(相對於物體而言)要比從後面撞擊物體的微粒速度更高——這種作用將減小太陽和地球的距離。該拖曳阻力的大小與 vu 成正比,其中 v 是粒子的速度,u 是物體的速度,而重力則與 v2 成正比,因此阻力與重力的比值與 u/v 成正比。因此,對於給定的重力強度,可以通過增加超凡小體的速度 v 來任意減小給定速度 u 下的阻力。然而,為了將阻力減小到經典力學上可接受的水平(即與觀察結果一致),速度 v 必須比光速大許多個數量級。這使得勒薩吉理論與基於狹義相對論的現代力學從根本上不相容,因為根據後者,任何粒子(或波)都不能超過光速。另外,即使有可能是超光速微粒,這種微粒流的有效溫度也足以在短短的幾分之一秒內焚燒所有一般物質。
軌道畸變
如拉普拉斯所證明的,另一種在勒薩吉模型中可能由於有限引力速度引起的效應是軌道的畸變(aberration)。除非勒薩吉微粒以遠大於光速的速度運動——像勒薩吉或開爾文所認為的那樣——否則物體之間的相互作用會存在時間延遲(即存在非零的傳輸時間)。在軌道運動的情況下,這會導致物體對另一個物體一段時間前的位置做出反應,從而對另一個物體產生一個切向力分量。與拖曳效應相反,這一分力將使兩個對象加速相互遠離。為了保持穩定的軌道,引力的作用必須比光速快得多,或引力並非純粹的中心力。許多人認為這是對任何勒薩吉式理論的決定性駁斥。相反,廣義相對論與拉普拉斯未觀察到明顯像差的結果一致,因為即使重力僅以光速傳播,在廣義相對論下,預期的軌道畸變也幾乎完全被相互作用中與速度有關的項所抵消。[51]
重力的範圍
在許多微粒模型中,例如開爾文的微粒模型中,由於微粒之間相互作用的性質,重力的範圍會受到限制。在這些模型中,微粒通過物質而產生的動量虧損(遮蔽)會轉變為模型假定的其他運動模式,而這種運動模式又會使微粒相互碰撞時回復其原來的動量(使得遮蔽的陰影“模糊”),故重力的範圍會取決於這種碰撞的速率,或者在有效意義上取決於微粒的平均自由程。也因此,在這些模型中關於重力有效範圍的預測將有所變化,取決於對粒子相互作用可能模式的特定方面和其他特殊假設。但是,對於這類模型,已觀察到的宇宙大尺度結構,例如銀河系,表明重力的有效範圍至少要有數百萬光年,否則無法容許這些結構存在。這是對這種粒子散射模型的限制。
吸收
如歷史部分所述,所有勒薩吉式模型的共同主要問題是能量和熱的問題。正如馬克士威和龐加萊所表明的,非彈性碰撞會導致物質在幾分之一秒內蒸發,而已提出的解決方案並不令人信服。例如,Aronson[30] 給馬克士威的斷言做了更簡單的證明:
| 假設與馬克士威的預設相反,物質分子實際上比粒子具有更多的能量。在這種情況下,粒子平均來說會在碰撞中獲得能量,而被另一物體 B 攔截的粒子,將被從物體 B 反彈的更具能量的粒子所代替。如此一來,重力的作用將被逆轉:與觀察相反,物體之間將會產生斥力。另一方面,如果粒子和分子的平均動能相同,則不會發生淨能量轉移,並且碰撞將等同於彈性碰撞,這時正如已經證明的那樣,不會產生引力。 |
同樣,艾森卡赫違反能量守恆定律也是不可接受的,開爾文對克勞修斯定理的應用則(如開爾文本人所指出的)造成了某種永動機,也違反了能量守恆定律。波模型的二次再輻射機制引起了湯姆森的興趣,但是馬克士威或龐加萊並沒有非常重視,因為它嚴重違反了熱力學第二定律(大量能量自發地被吸收了,從較冷的形式轉換為較熱的形式),而這是所有物理定律中最牢固的一種。
這一能量問題也被膨脹地球說的支持者考慮,和他們認為存在質量吸積的觀念相連(即地球通過引力吸引積累周圍物質而膨脹)。早期將膨脹地球說與某種形式的推力重力下質量增加聯結在一起的理論家包括亞爾科夫斯基(Ivan Osipovich Yarkovsky)與希爾根貝格(Ott Christoph Hilgenberg)[52]。主流科學家已不再認為質量吸積或膨脹地球說的觀念是有效的,其中一個理由是根據質能等價原理,如果地球吸收超凡小體流的能量來產生我們觀察到的引力(使用龐加萊計算的能量值),則其質量將會在幾分之一秒內倍增。
原子結合能
根據觀察證據,現在知道重力與所有形式的能量相互作用,而不僅僅是與質量相互作用。原子核的靜電結合能,原子核中弱相互作用的能以及原子中電子的動能都對原子的引力質量有貢獻,這已在厄缶型實驗中以高精確度得到證實。[53]這同時意味著一定數量的氣體的原子運動得更快時,該氣體的引力會增加。此外,月球雷射測距實驗表明,甚至引力結合能本身也具有引力,其強度與等效原理的預測以高精確度一致——進一步證明,任何成功的引力理論都必須是非線性的,而且具有自耦合性。[54] [55]勒薩吉的理論沒有預測上述影響的任何一部份,其理論的任何已知變體也都沒有預測。
重力以外的應用與類比
仿重力
萊曼·史匹哲(Lyman Spitzer)在 1941 年[56]計算得出兩個塵埃粒子吸收彼此之間的輻射會導致與 1/r2 成正比的淨吸引力(顯然他沒有意識到了勒薩吉式的遮蔽機制,也沒有注意到洛倫茲將輻射壓力和重力類比的考慮) 。喬治·伽莫夫(George Gamow)將此效應稱為“仿重力”。他於1949年提出[57]在大霹靂之後,電子的降溫速度可能快於背景輻射的降溫速度,而電子間輻射的吸收會導致勒薩吉式機制,這可能在大霹靂後不久的星系形成過程中發揮重要作用。然而,該猜測在 1971 年被 Field 否決了,[58]他表明這種影響太小,因為電子和輻射實際上幾乎處於熱平衡狀態。1986 年,Hogan 和 White 認為[59] ,仿重力可能通過吸收星系形成前的星光影響了星系的形成。但 Wang 和 Field 又證明[60]任何形式的模擬引力都無法產生足夠的力來影響星系的形成。
等離子體
勒薩吉式機制也被認為是粉塵等離子體(dusty plasma)行為的重要因素。A.M. Ignatov[61] 證明了,由於等離子和塵埃離子之間的非彈性碰撞,在各向同性無碰撞等離子體中懸浮的兩個塵埃顆粒間會產生吸引力。該吸引力與塵粒間距離的平方成反比,並且可以抵消塵粒間的庫侖排斥力。
晚近發展
勒薩吉理論在 19 世紀得到的重新評估發現了與該理論緊密相關的幾個問題,包括過度加熱、拖曳阻力、重力屏蔽和軌道畸變。對這些問題的認識,以及注意力從重力的機械解釋普遍移走,導致人們對勒薩吉理論的興趣逐漸喪失。最終在 20 世紀,愛因斯坦的廣義相對論使勒薩吉的理論黯然失色。
1965 年,理察·費曼(Richard Feynman)檢視了法蒂奧—勒薩吉機制,主要是把它當做範例,說明如何不用複雜數學,用較簡單的操作來解釋“複雜的”物理定律(在這種情況下,是指牛頓的平方反比定律),同時作為失敗理論的示例。他指出,“彈跳粒子”的機制再現了平方反比定律,並且“奇異的數學關係大大減少”,但隨後指出,該方案“不起作用”,因為它預言運動的物體會受到拖曳阻力。[62][63]
儘管它在主流科學界中被認為是不可行的理論,但偶爾也有人嘗試在主流之外復興該理論,包括 Radzievskii 與 Kagalnikova (1960),[64]Shneiderov (1961),[65]Buonomano 與 Engels (1976),[66]Adamut (1982),[67]Ioan-Iovitz Popescu (1982),[68]Jaakkola (1996),[69]Tom Van Flandern (1999),[70]Borge (2002),[71]Edwards (2007),[72]以及 Eid (2016)。[73]
Edwards 等人[74] 也討論了各種勒薩吉模型和相關主題。
最近有一份有關新型定量推力理論的工作論文準備驗證[75],該論文發表在CERN尚未引用的Zenodo平台上。
腳註
- 指用基本的簡單機械過程來解釋物理現象產生的理論。
- Duillier, N. Fatio de, , Société Hollandaise des Sciences (编), 9, The Hague: 381–389, 1690a1888–1950 [2019-12-02], (原始内容存档于2020-11-16)
- 見參考文獻中的 Prévost (1805)。
- Duillier, N. Fatio de, , Bopp, Karl (编), , Schriften der Straßburger Wissenschaftlichen Gesellschaft in Heidelberg 10 (Berlin & Leipzig), 1701, 10: 19–661929
- Duillier, N. Fatio de, Gagnebin, Bernard , 编, , Notes and Records of the Royal Society of London, 1743, 6 (2): 125–1601949, doi:10.1098/rsnr.1949.0018
|chapter=被忽略 (帮助) - Zehe (1980),見參考文獻
- Cramer, G., , Geneva, 1731
- Redeker, F. A., , Lemgoviae Ex Officina Meyeriana, 1736
- “死力”是萊布尼茲用的詞語,類似於今天所說的位能,與之相對的“活力”則類似於今天的動能。
- Georges-Louis Le Sage, , Mercure de France, 1756: 153–171
- Sage, G.-L. Le, , Not published – private print, 1761 [2019-12-02], (原始内容存档于2020-12-05)
- Sage, G.-L. Le, , Memoires de l'Academie Royale des Sciences et Belles Lettres de Berlin, 1784: 404–432 [2020-06-01], (原始内容存档于2008-06-17),英文翻譯可見於Sage, G.-L. Le, , Langley, Samuel P. (编), , Annual Report of the Board of Regents of the Smithsonian Institution, June 30, 1898: 139–160
- Sage, G.-L. Le, , Prévost, Pierre (编), , Geneva & Paris: J.J. Paschoud: 1–186, 1818
- Wolf (1852),見參考文獻
- Evanes (2002),見參考文獻
- Playfair (1807),見參考文獻
- Lichtenberg, G. C., Zehe, H.; Hinrichs, W. , 编, , Nachrichten der Akademie der Wissenschaften zu Göttingen, II. Mathematisch-physikalische Klasse (1), 2003, (1)
- Lichtenberg, in German: "Ist es ein Traum, so ist es der größte und erhabenste der je ist geträumt worden, und womit wir eine Lücke in unseren Büchern ausfüllen können, die nur durch einen Traum ausgefüllt werden kann".
- Kant, I., : Dynamik, Lehrsatz 5, 1786 [2019-12-02], (原始内容存档于2019-09-13)
- Schelling, F.W.J., , 1797 [2019-12-02], (原始内容存档于2017-04-24)
- Laplace, P.-S. . 4. Chelsea, New York. 1966 [1805].
|issue=被忽略 (帮助) - Leray, le P., , Comptes Rendus, 1869, 69: 615–621 [2019-12-02], (原始内容存档于2020-01-25)
- Thomson, William (Lord Kelvin), , Phil. Mag., 1873, 45: 321–332, doi:10.1080/14786447308640865
- Tait, P. G., , London: Macmillan and Co., 1876, hdl:2027/mdp.39015064456968

- 這一評論與開爾文自己相信的理論有關係,他認為原子是以太的渦旋。
- Kelvin, Popular Lectures, vol. i. p. 145.
- Preston, S. T., , Phil. Mag., 5th Series, 1877, 4: 206–213 (pt. 1) and 364–375 (pt. 2), doi:10.1080/14786447708639322
- Drude (1897),見參考文獻
-
 Maxwell, J. C., , Baynes, T.S. (编), 3 9th, New York: Charles Scribner's Sons: 38–47, 1878
Maxwell, J. C., , Baynes, T.S. (编), 3 9th, New York: Charles Scribner's Sons: 38–47, 1878 - (Aronson 1964),見參考文獻
- Isenkrahe, C., , Braunschweig: Friedrich Vieweg und Sohn, 1879
- Ryšánek, A., Repert. Exp. Phys., 1887, 24: 90–115 缺少或
|title=为空 (帮助) - Bois-Reymond, P. du, , Naturwissenschaftliche Rundschau, 1888, 3 (14): 169–176
- Keller, F.A.E; Keller, Ém., , Comptes Rendus, 1863, 56: 530–533 [2019-12-02], (原始内容存档于2020-01-25)
- Boisbaudran, Lecoq de, , Comptes Rendus, 1869, 69: 703–705 [2019-12-02], (原始内容存档于2020-01-25)
- Lorentz, H. A., , Proc. Acad. Amsterdam, 1900, 2: 559–574 [2019-12-02], (原始内容存档于2021-01-15)
- Lorentz, H. A., , London: Macmillan and Co., 1927 [1922]
- Corry (1999),見參考文獻
- Thomson, J. J., , Westminster: Archibald Constable & Co., Ltd., 1904
-
 Thomson, J. J. . Chisholm, Hugh (编). 17 (第11版). London: Cambridge University Press: 895. 1911.
Thomson, J. J. . Chisholm, Hugh (编). 17 (第11版). London: Cambridge University Press: 895. 1911. - Tommasina, T., , Paris: Gauthier-Villars, 1928
- Brush, C. F., , Nature, 1911, 86 (2160): 130–132, Bibcode:1911Natur..86..130., doi:10.1038/086130a0
- Darwin, G. H., , Proceedings of the Royal Society, 1905, 76 (511): 387–410 [2019-12-02], Bibcode:1905RSPSA..76..387D, doi:10.1098/rspa.1905.0042, (原始内容存档于2017-07-26)
- Darwin, G. H., , 1916
- Poincaré, Henri, , , New York: Science Press: 517–522, 1913
- Feynman, R. P., , Addison-Wesley: 23–28, 1995
- Bertolami, O; Paramos, J; et al. . 2006. arXiv:gr-qc/0602016
 .
. - Martin (1999),見參考文獻
- Martins (2002),見參考文獻
- Borzeskkowski et al. (2004),見參考文獻
- Carlip, S., , Phys. Lett. A, 2000, 267 (2–3): 81–87, Bibcode:2000PhLA..267...81C, arXiv:gr-qc/9909087
 , doi:10.1016/S0375-9601(00)00101-8
, doi:10.1016/S0375-9601(00)00101-8 - Scalera, G.; Jacob, K.-H. (编), , Rome: INGV, 2003
- Carlip, S., , Am. J. Phys., 1998, 65 (5): 409–413, Bibcode:1998AmJPh..66..409C, arXiv:gr-qc/9909014
 , doi:10.1119/1.18885
, doi:10.1119/1.18885 - Adelberger, E.G.; Heckel, B.R.; Smith, G.; Su, Y.; Swanson, H.E., , Nature, Sep 20, 1990, 347 (6290): 261–263, Bibcode:1990Natur.347..261A, doi:10.1038/347261a0
- Williams, J.G.; Newhall, X.X.; Dickey, J.O., , Phys. Rev. D, 1996, 53 (12): 6730–6739, Bibcode:1996PhRvD..53.6730W, doi:10.1103/PhysRevD.53.6730
- Spitzer, L., , The Astrophysical Journal, 1941, 94: 232–244, Bibcode:1941ApJ....94..232S, doi:10.1086/144328.
- Gamow, George, , Reviews of Modern Physics, 1949, 21 (3): 367–373, Bibcode:1949RvMP...21..367G, doi:10.1103/RevModPhys.21.367.
- Field, G. B., , The Astrophysical Journal, 1971, 165: 29–40, Bibcode:1971ApJ...165...29F, doi:10.1086/150873.
- Hogan, C.J., , The Astrophysical Journal, 1989, 340: 1–10, Bibcode:1989ApJ...340....1H, doi:10.1086/167371.
- Wang, B.; Field, G.B., , The Astrophysical Journal, 1989, 346: 3–11, Bibcode:1989ApJ...346....3W, doi:10.1086/167981.
- Ignatov, A.M., , Plasma Physics Reports, 1996, 22 (7): 585–589, Bibcode:1996PlPhR..22..585I
- Feynman, R. P., , Cambridge, Mass.: Massachusetts Institute of Technology: 37–39, 1967, ISBN 0-262-56003-8
- Feynman's description of Le Sage's theory starts 7 minutes into this video clip (页面存档备份,存于)
- Radzievskii, V.V.; Kagalnikova, I.I., , Vsesoyuz. Astronom.-Geodezich. Obsch. Byull., 1960, 26 (33): 3–14 A rough English translation appeared in a U.S. government technical report: FTD TT64 323; TT 64 11801 (1964), Foreign Tech. Div., Air Force Systems Command, Wright-Patterson AFB, Ohio (reprinted in Pushing Gravity)
- Shneiderov, A. J., , Bollettino di Geofisica Teorica ed Applicata, 1961, 3: 137–159
- Buonomano, V.; Engel, E., , Int. J. Theor. Phys., 1976, 15 (3): 231–246, Bibcode:1976IJTP...15..231B, doi:10.1007/BF01807095
- Adamut, I. A., , Nuovo Cimento C, 1982, 5 (2): 189–208, Bibcode:1982NCimC...5..189A, doi:10.1007/BF02509010
- Popescu, I. I., , Romanian Academy Journal of Physics, 1982, 34: 451–468. Translation published as (PDF), [2019-12-02], (原始内容存档 (PDF)于2016-01-13), Contemporary Literature Press, 2015. ISBN 978-606-760-009-4
- Jaakkola, T., (PDF), Apeiron, 1996, 3 (3–4): 61–75 [2019-12-02], (原始内容存档 (PDF)于2019-10-24)
- Flandern, T. Van, 2, Berkeley: North Atlantic Books: Chapters 2–4, 1999
- Borge, C. J., , São Paulo, Brazil.: Do Autor: 1–150, 2002, ISBN 8-590-26831-4
- Edwards, M .R., (PDF), Apeiron, 2007, 14 (3): 214–233 [2019-12-02], (原始内容存档 (PDF)于2019-03-03)
- Eid, C.O., (PDF), Fundamental Journals, 2016 [2016-04-27], (原始内容 (PDF)存档于2018-06-03)
- Edwards, M. R. (编), , Montreal: C. Roy Keys Inc., 2002
- Danilatos, G., , Zenodo, 2020 [2020-12-21], doi:10.5281/zenodo.4284106, (原始内容存档于2020-12-10)
參考文獻
- Aronson, S., , The Natural Philosopher, 1964, 3: 51–74 [2019-12-02], (原始内容存档于2006-03-05)
- Bellone, E., , Mem. Società Astronomica Italiana, 1991, 62 (3): 477–485, Bibcode:1991MmSAI..62..477B
- Borzeszkowski, H.-H.; Chrobok, T.; Treder, H.-J., G. T. Gillies; V. N. Melnikov; V. de Sabbata , 编, , Proceedings of the 18th Course of the School on Cosmology and Gravitation, 2004: 1–37, Bibcode:2004grco.book....1V, ISBN 978-1-4020-1956-2, arXiv:gr-qc/0310081
 , doi:10.1007/978-1-4020-2242-5_1
, doi:10.1007/978-1-4020-2242-5_1 |contribution=被忽略 (帮助) - Chabot, H., (PDF), Actes des Journées de Peirescq "La pensée numérique", Sciences et Techniques en Perspective, 2ème série, 2004, 8: 179–198 [2019-12-02], (原始内容 (PDF)存档于2017-04-24)
- Corry, L., (PDF), Archive for History of Exact Sciences, 1999, 53 (6): 489–527 [2019-12-02], doi:10.1007/s004070050005, (原始内容存档 (PDF)于2020-09-25)
- Drude, Paul, , Annalen der Physik, 1897, 298 (12): I–XLIX [2019-12-02], Bibcode:1897AnP...298D...1D, doi:10.1002/andp.18972981220, (原始内容存档于2020-09-28)
- Evans, J. C., , Edwards, M.R. (编), , Montreal: C. Roy Keys Inc.: 9–40, 2002
- Martins, de Andrade, R., , Goemmer, H.; Renn, J.; Ritter, J. (编), 7, Boston: Birkhäuser: 3–44, 1999 [2019-12-02], (原始内容存档于2010-08-09)
- Martins, de Andrade, R., , Edwards, M.R. (编), (PDF), Montreal: C. Roy Keys Inc.: 239–258, 2002 [2019-12-02], (原始内容 (PDF)存档于2004-07-25)
- Playfair, J., , Edinburgh Review, 1807: 137–153 English summary of Prévost (1805).
- Prévost, P. (编), , Geneva & Paris: J.J. Paschoud, 1805 [2019-12-02], (原始内容存档于2007-11-12)
- Rowlinson, J. S., , Notes Rec. R. Soc. Lond., 2003, 57 (1): 35–45, doi:10.1098/rsnr.2003.0195
- Taylor, W. B., , Annual Report of the Smithsonian Institution, 1876, 31: 205–282
- Wolf, R., , Biographien zur Kulturgeschichte der Schweiz (Orell, Füssli & co.), 1862, 4: 173–192 [2019-12-02], (原始内容存档于2012-11-11)
- Zehe, H., , Hildesheim: Gerstenberg, 1980, ISBN 3-8067-0862-2
- Zenneck, J., , Encyklopädie der Mathematischen Wissenschaften mit Einschluss Ihrer Anwendungen (Leipzig), 1903, 5 (1): 25–67 [2019-12-02], ISBN 978-3-663-15445-7, doi:10.1007/978-3-663-16016-8_2, (原始内容存档于2021-03-12)