卡諾定理 (垂線)

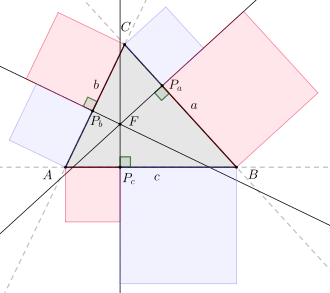
對於一個三角形${\displaystyle ABC}$，其三邊為${\displaystyle a,b,c}$。考慮三條垂直於各邊且交於一點的直線，若${\displaystyle P_{a},P_{b},P_{c}}$是這三條垂線在${\displaystyle a,b,c}$上的垂足，則下列關係式成立：

${\displaystyle |AP_{c}|^{2}+|BP_{a}|^{2}+|CP_{b}|^{2}=|BP_{c}|^{2}+|CP_{a}|^{2}+|AP_{b}|^{2}}$

該命題的逆命題同樣成立：若${\displaystyle P_{a},P_{b},P_{c}}$在邊上的位置滿足關係式，則以這三點為垂足做出的三條垂線會交於一點。因此，該關係式為垂線是否交於一點提供了一個充分必要條件。

若三角形${\displaystyle \triangle ABC}$的角${\displaystyle C}$為直角，則可以將三條垂線的交點${\displaystyle F}$置於${\displaystyle A}$上。此時由於${\displaystyle P_{a}=C}$、 ${\displaystyle P_{b}=A}$且${\displaystyle P_{c}=A}$，可得${\displaystyle |AP_{b}|=0}$、${\displaystyle |AP_{c}|=0}$、${\displaystyle |CP_{a}|=0}$、${\displaystyle |CP_{b}|=b}$、${\displaystyle |BP_{a}|=a}$與${\displaystyle |BP_{c}|=c}$，代入卡諾定理的關係式後，即可推得畢氏定理${\displaystyle a^{2}+b^{2}=c^{2}}$。

若三條垂線皆為中垂線，則${\displaystyle |AP_{c}|=|BP_{c}|}$、${\displaystyle |BP_{a}|=|CP_{a}|}$且${\displaystyle |CP_{b}|=|AP_{b}|}$，無論三邊長度為何，上述關係式必會成立，故可推得三角形的三條中垂線必交於一點。

• Wohlgemuth, Martin. (编). . Heidelberg: Spektrum Akademischer Verlag. 2010: 273–276. ISBN 9783827426079. OCLC 699828882 （German）. 引文格式1维护：未识别语文类型 (link)
• 阿爾弗雷德·S·波薩門蒂; Charles T. Salkind. . New York: Dover. 1996: 85–86. ISBN 9780486134864. OCLC 829151719.