双棘轮算法

KDF链是双棘轮算法中的核心概念。KDF是这样一个密码学函数：输入一个秘密且随机的KDF密钥（KDF key）及其它一些输入数据，并返回输出数据。在密钥未知的前提下，输出的数据与随机数不可区分（也就是说，KDF满足密码学「PRF」的要求）。若密钥不是秘密且随机的，则KDF应仍然能作为密钥和输入数据的安全的密码学哈希。当HMAC和HKDF使用安全的哈希算法实例化时，二者的构造即满足KDF定义。[4][5]

我们使用术语KDF链（KDF chain）表示如下流程：一个KDF输出的一部分作为输出密钥（Output key），而另一部分将取代KDF密钥，作为另一个KDF的输入密钥。

一个处理三个输入密钥并生成三个输出密钥的KDF链

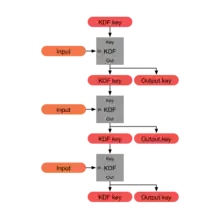
一个KDF链具有如下特性[6]：

• 弹性（resilience）：对于不知道KDF密钥的攻击者来说，输出密钥看起来是随机的。即使攻击者能控制KDF的输入，此条特性仍然成立。
• 前向安全性：对于知道某一时刻的KDF密钥的攻击者来说，旧的输出密钥看起来是随机的。
• 被攻破后的可恢复性（break-in recovery）：对于知道某一时刻的 KDF 密钥的攻击者来说，新的输出密钥看起来是随机的，只要新的输入中增加了足够的熵（entropy）。

在Alice和Bob之间的双棘轮会话中，双方保存的KDF密钥将用于三条链：根链（root chain）、发送链（sending chain）及接收链（receiving chain），Alice的发送链对应Bob的接收链，反之亦然。

Alice和Bob交换消息的同时，也交换新的迪菲-赫尔曼公钥，而迪菲-赫尔曼输出的密钥将作为根链的输入。根链输出的密钥将作为发送链和接收链的KDF密钥。这称为迪菲-赫尔曼棘轮（Diffie-Hellman ratchet）。

每发送和接收一条消息，发送链和接收链都将向前推进。相应的输出密钥将用于加密和解密消息。这称为对称密钥棘轮（symmetric-key ratchet）。

每条发送或接收的消息都使用一个唯一的消息密钥（message key）加密。消息密钥是发送KDF链和接收KDF链的输出密钥。这些链的KDF密钥称为链密钥（chain key）。

由于发送链和接收链的KDF输入是常数，所以这两条链不具备被攻破后的可恢复性。发送链和接收链只能确保每条消息使用唯一的密钥加密，而此密钥在加密或解密后可以删除。由一个给定的链密钥计算下一个链密钥和消息密钥的过程，称为对称密钥棘轮（symmetric-key ratchet）的棘轮步进（ratchet step）。

对称密钥棘轮的两次棘轮步进

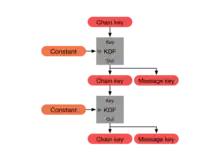
由于消息密钥不用于派生其它密钥，因此可以保存起来而不影响其它消息密钥的安全性。这将有助于处理消息的丢失或乱序。

如果中间攻击者窃取了其中一方的发送链密钥和接收链密钥，那么他可以计算此后所有的消息密钥，并解密对应的消息。为了避免这种情况，双棘轮算法将对称密钥棘轮与DH棘轮组成在一起，使用后者基于迪菲-赫尔曼的输出更新链密钥。

为了实现DH棘轮，通信双方各自生成一个DH密钥对（迪菲-赫尔曼公钥和私钥）作为当前的棘轮密钥对（ratchet key pair）。从任意一方发出的每一条消息都将携带一个消息头，其中包含发送者当前的棘轮公钥。当接收到远端发送过来的新的棘轮公钥时，本端将实施一次DH棘轮步进（DH ratchet step），生成一个新的棘轮密钥对以取代本端当前的密钥对。

通信双方交替地更新棘轮密钥对，使之形成一个「乒乓」行为模式。仅截获了其中一方的窃听者可能得到当前棘轮私钥的值，但此棘轮私钥将最终被未泄露的棘轮私钥取代。那时，棘轮密钥对之间的迪菲-赫尔曼计算将定义一个对攻击者未知的新的DH输出。

将对称密钥棘轮和 DH 棘轮组合在一起，形成了双棘轮：

• 当发送或接收消息时，执行一次发送链或接收链的对称密钥棘轮步进，以派生新的消息密钥。
• 当接收到新的棘轮公钥时，在对称密钥棘轮步进之前，执行一次 DH 棘轮步进，以更新链密钥。