反德西特空間

托里拆利小號

• 最大對稱勞侖茲流形：類似於廣義相對論的時空，其中時間與空間在各方向都是數學上等價。
• 常數純量曲率：類似於廣義相對論中重力造成時空彎曲，而在此情形下無物質或能量，曲率在時空中各處皆為單一數值。
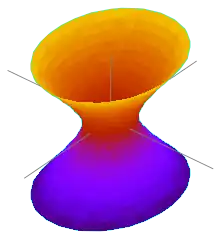
• 負曲率：類似雙曲空間的彎曲方式，形似托里拆利小號或馬鞍面；與球面的正曲率情形相反。負曲率對應到吸引力，而正曲率對應到排斥力。
• 量子場論：描述基本作用力（比如電磁力、弱作用力、強作用力）的量子理論。
• AdS/CFT對偶：由胡安·馬爾達西那於1997年提出，闡述了四維時空中以量子場論描述的作用力可用弦論來描述，而弦處在多一維度的反德西特空間中。此對偶關係的重要性在於其陳述了量子場論可以用幾何方式表示，有別於以往的陳述方式。
• 共形場論：具有純量不變性的量子場論。

廣義相對論是描述時間、空間與重力之間關係的理論，其中重力是時空因物質或能量存在而彎曲的表現。質量與能量是等價，兩者關係式為

　${\displaystyle E=mc^{2}}$，

其中c為真空中光速。而時間與空間也是等價的，透過c可使兩者單位一致。

廣義相對論的效果常用一個類比方式來說明：一張彈性墊因為上面的重物而凹陷，經過重物附近的小球的行進路徑因此受到影響，發生了路徑的偏折。這樣的效果在牛頓力學中視為一種「吸引力」。而「吸引力」是物體造成時空負曲率的表現；在彈性墊的例子，負曲率即類似於托里拆利小號形狀的凹陷。廣義相對論的特色也在於其將重力描述時空的彎曲，而非傳統對力的描述（例如：電磁力）。

彈性墊的例子描述了二維空間因重力發生彎曲，背景為一個三維超空間，而第三維度對應到重力的影響。現實生活中則可類比地想作四維時空因重力發生彎曲，背景為五維超空間，而第五維度對應到重力與相關效應的影響。

較為大眾所熟悉的牛頓萬有引力定律

${\displaystyle \textstyle F=G{\frac {m_{1}m_{2}}{r^{2}}}\ }$

所描述的兩物體因具有質量而彼此吸引，僅是廣義相對論中重力效應的近似，在極端情形下則會失去預測精準度。兩者其中之一差異在於廣義相對論中，時空一同彎曲，而非僅只空間彎曲。平常情形下，時間的彎曲程度太小，以至於儀器無法區分牛頓重力理論與廣義相對論的差別。

正常的德西特空間與廣義相對論時空最基礎的差義在於：即使沒有物質或能量存在，德西特空間仍有一些些的彎曲。如此內生性的時空曲率可與宇宙常數以及暗能量的概念相連結。

類似於之前的例子，關於德西特空間一個常用的類比為：彈性墊置於一球面上而發生些微的彎曲，因為球面極大而此曲率很小。空的德西特空間帶有些微排斥力，物質間的萬有引力與此排斥力相抵抗。正常德西特空間對應到正的宇宙常數，與目前天文學觀測相符，而宇宙常數的值與德西特空間的曲率等價。從另個角度來看，德西特空間的「自身能量」造成了宇宙加速膨脹。

反德西特空間與正常的德西特空間相異，在不存在物質或能量的情形下，時空曲率是呈現雙曲形式的。

運用上面的類比例子：想像一塊彈性墊置放於鞍面上而產生彎曲，因為這個鞍面極大所以彎曲程度極小。如此對應到負值宇宙常數，目前在現實生活中尚未觀測到此現象。反德西特空間的效果是宇宙會加速塌縮。

一如正常德西特空間，反德西特空間的曲率與宇宙常數等價，儘管數值上兩者分別為一正一負。