反餘割

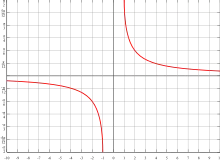
反餘割（英語：、記為：${\displaystyle \operatorname {arccsc} }$或${\displaystyle \csc ^{-1}}$）是一種反三角函數[3]，對應的三角函數為餘割函數，用來計算已知斜邊與對邊的比值求出其夾角大小的函數，是高等數學中的一種基本特殊函數，其輸入值與反正弦互為倒數。

反餘割
性質
奇偶性	奇函数
定義域	${\displaystyle \left\{x\in \mathbb {R}$ :\left|x\right|\geq 1\right\}} [1]
到達域	${\displaystyle \left\{y\in \mathbb {R}$ :-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}\land y\neq 0\right\}} ${\displaystyle \left\{y\in \mathbb {R}$ :-90^{\circ }\leq y\leq 90^{\circ }\land y\neq 0\right\}}
周期	N/A
特定值
當x=0	不存在[註 1]
當x=+∞	0
當x=-∞	0
當x=1	${\displaystyle -{\frac {\pi }{2}}}$ （-90°）
當x=-1	${\displaystyle {\frac {\pi }{2}}}$ （90°）
其他性質
渐近线	${\displaystyle y=0}$
不動點	±1.11415714087193...

原始的定義是將餘割函數限制在${\displaystyle [-{\frac {\pi }{2}},{\frac {\pi }{2}}]}$（[-90°, 90°]）的反函數
在複變分析中，反餘割是這樣定義的：

${\displaystyle \operatorname {arccsc} x=-{i}\ln \left({\tfrac {i}{x}}+{\sqrt {1-{\tfrac {1}{x^{2}}}}}\right)\,}$

這個動作使反餘割被推廣到複數。

下圖表示推廣到複數的反餘割複數平面函數圖形，可以見到圖中央有一條明顯的橫線正好是實數中未被定義的區間${\displaystyle [-1,1]}$。

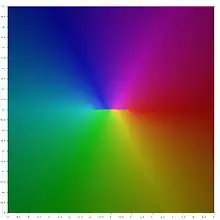
拓展到複數的反餘割函數