吴氏实验
吴氏实验是由美籍华裔物理学家吴健雄与美国国家标准局低温研究组合作进行的一项核物理学实验[1]。这一实验的目的在于验证弱相互作用中宇称是否守恒。此前,人们已经确认电磁相互作用及强相互作用中宇称确实守恒,但弱相互作用中是否仍然守恒,尚没有实验进行验证。在宇称守恒情况下,一个系统在进行镜像变换后,其物理行为也会随之发生镜像变换。从表观来看,系统在变换后只是左右相反,其余与原来无异。而如果宇称不守恒,则在镜像变换前后,除了左右相反外,系统的行为相对于原来还会存在其他差异。
_in_1963.jpg.webp)
这项实验验证了弱相互作用中宇称不守恒。这项结果此前已由李政道与杨振宁从理论上导出。他们还提出了验证此项结果的实验方案。二人因为这项理论成果获得1957年的诺贝尔物理学奖。
历史
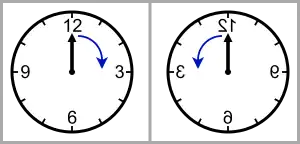
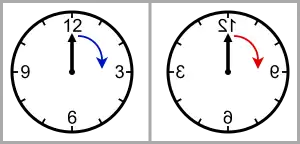
1927年,尤金·维格纳提出了宇称守恒原理[2],即系统在经过镜像变换前后运动规律基本保持不变,只是左右相反,例如顺时针旋转的表针在经过镜像变换后则会逆时针旋转。
这项原理得到物理学家的普遍认同,且经过实验证实在电磁相互作用及强相互作用中成立。但到了20世纪50年代中期,当时观察到的一些现象展示着这一原理在弱相互作用中可能并不成立。其中较为有代表性的现象就是Θ-τ问题。
Θ+
和
τ+
是两种性质几乎完全相同的奇介子,它们惟一的不同就是发生衰变后终态的宇称不相同。[3]如果宇称守恒的话,那么
Θ+
和
τ+
会发生如下的衰变:
Θ+→
π+
+
π0
τ+→
π+
+
π+
+
π−
1956年,理论物理学家李政道和杨振宁发表了一篇文獻評論,其研討有关宇称守恒定律在各種基礎相互作用裏是否成立的論題。他們總結,對於弱相互作用案例,實驗數據尚未確認或否定宇称守恒定律,并设计了相关的实验验证方案。[4]不久后,他们与β衰变方面的专家吴健雄联系,向她叙述了几个实验验证思路。他们最终决定测定钴-60发生β衰变时的取向性质。吴健雄随后经由精通低温物理學的亨利·布爾斯與马克·泽曼斯基接触到美国国家标准局的相关人士。相关实验被安排在1956年12月于国家标准局低温实验室中进行。[3]
李杨二人在该实验完成并验证他们的理论预测后不久于1957年获授诺贝尔物理学奖。[5]
实验

吴健雄的实验团队在实验中观测了稳恒磁场中冷却至绝对零度附近的钴-60原子的衰变情况。[3]钴-60是一种不稳定的钴同位素,其会发生β衰变转变为稳定的镍-60。在发生衰变时,钴-60核中的一个中子会衰变为一个质子,同时放出一个电子与一个反电中微子。衰变后产生的镍-60核处于激发态,它会放出两束γ射线从而返回基态。因此该核反应全程的方程式为:
γ射线是一种光子,它们自镍-60核释出的过程是一种电磁作用过程。由于电磁作用遵守宇称守恒,因而对其分布的观测对于本实验而言非常重要。具体来说,在本实验中γ射线的分布情况被用来间接反映钴-60核的极化情况以及实验系统的温度。在吴氏实验中,实验团队对于自旋取向相反的钴-60核的电子释出情况进行了比较。如果放出的电子的分布与自旋取向存在不对称性,那么该过程宇称不守恒。
实验材料与实验方法
.png.webp)
本项实验所存在的一个挑战就是如何尽可能地增加钴-60核的极化率。由于原子核的磁矩相对于电子而言非常的小,因而为实现上述目标,则需要将实验系统置于强磁场中,而实验环境的温度也需要非常低,远远低于单独依靠液氦冷却所能达到的低温。在本实验中,该低温环境是通过绝热去磁法获取的。在实验中,实验人员将放射性的钴制成一层薄膜放置在铈镁硝酸盐表面。在实验所要求的低温环境中,这种顺磁性物质具有高度各向异性的朗德g因子。实验人员先将铈镁硝酸盐沿着g因子较大的轴磁化,然后通过液氦将系统冷却至1.2 K,然后去除水平磁场,令实验系统进一步冷却至0.003 K。为留出用于极化钴核的垂直线圈的空间,水平磁体被分开放置。由于对应方向上铈镁硝酸盐的g因子较小,因而垂直线圈的磁场对于温度产生的影响基本可以忽略。这种令钴-60高度极化的方法源于科内利斯·雅各布斯·戈特[6]及M·E·罗斯[7]的研究结果。
用于表征极化情况的γ射线则是由位于实验系统赤道面与极点方向的计数器进行监视。实验人员会在实验开始后15分钟内持续监视γ射线的分布情况,而在这段时间内晶体的温度会逐渐上升,各向异性也会随之消失。实验人员也会在同一时段持续监视β射线的释出情况。[1]
实验结果
.jpg.webp)
如果β衰变遵守宇称守恒,电子的释出方向相对于核自旋取向而言并不会有一个從優的方向。然而,吴健雄等人却发现电子更倾向于沿着核自旋的反方向释出[1]。这一点相当程度上证明了β衰变并不遵守宇称守恒。[3][8]
这项实验结果在物理学界引起了一番轟动[3]。一些研究者试图去再现吴健雄的实验结果[9][10]。同时还有一些物理学家并不相信这一实验结果。当时在美国国家标准局工作的一名研究人员告诉沃尔夫冈·泡利宇称守恒可能并不时时成立。泡利回应了一句:“纯属无稽之谈。”而当那位研究人员告诉他吴健雄的实验结果确确实实地验证了这一点时,泡利则简单地回应了一句:“那么(这个结果)必须能够重现!”[3]至1957年底,吴健雄团队进一步进行的研究一再地验证了该结果。弱相互作用中宇称不守恒由此得到了有力的证明[3]。
现象机制与推论
吴氏实验找到一種操作定义“左”与“右”的方法。这种定义方法基于弱相互作用的固有性质。在此之前,“左”与“右”只是一个含混的概念,如果地球上的科学家与未曾谋面的另一星球上的科学家会面时,他们可能并不能了解彼此对于“左”与“右”的定义。吴氏实验的结果对于“左”与“右”给出了一个较为明确的定义,解决了奥兹玛问题。[11]
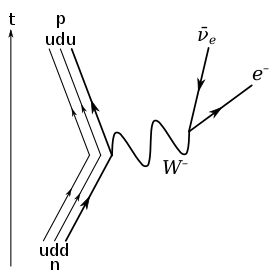
在基本粒子层面上,β衰变是由带负电的下夸克通过放出
W−
玻色子转换为带正电的上夸克引起的。
W−
玻色子会接着衰变为一个电子与一个反电中微子:
d
→
u
+
e−
+
ν
e.
当夸克在时空中传播时,其会在左手性与右手性间循环往复地振荡。從分析吴氏实验展示宇称不守恒的數據,可以推論,只有左手性的下夸克会参与弱相互作用,同时整个过程只会涉及左手性的夸克与轻子(或右手性的反夸克与反轻子)。右手性的粒子并不会参与弱相互作用。如果下夸克质量为零,那么其并不会发生振荡,右手性的下夸克自身则会十分的稳定。但正因为其具有质量,所以它有可能会发生振荡从而进一步发生衰变。[12]
从吴氏实验中还可以得到,无质量的中微子必定是左手性的,而无质量的反中微子必定是右手性的。由于物理学家通过实验已经证明中微子具有质量,因而右手性的中微子与左手性的反中微子也可以存在。这些中微子并不能与弱相互作用的拉格朗日量耦合,只能通过万有引力发生相互作用。它们可能是宇宙中暗物质的一种组分。[13]
参考文献
- Wu, C. S.; Ambler, E.; Hayward, R. W.; Hoppes, D. D.; Hudson, R. P. (PDF). Physical Review. 1957, 105 (4): 1413–1415 [2016-07-04]. Bibcode:1957PhRv..105.1413W. doi:10.1103/PhysRev.105.1413. (原始内容 (PDF)存档于2016-03-04) (英语).
- Wigner, E. P. . Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch Physikalische Klasse. 1927: 375–381 [2016-07-04]. (原始内容存档于2020-01-15) (德语).
- Reproduced in Wightman, A. S. (编). Vol. A. Springer. 1993: 84. ISBN 978-3-642-08154-5. doi:10.1007/978-3-662-02781-3_7.
- Hudson, R. P. . Lide, D. R. (编). (PDF). NIST Special Publication 958. National Institute of Standards and Technology. 2001 [2016-07-04]. ISBN 978-0849312472. (原始内容存档 (PDF)于2020-10-23) (英语).
- Lee, T. D.; Yang, C. N. (PDF). Physical Review. 1956, 104 (1): 254–258 [2016-07-04]. Bibcode:1956PhRv..104..254L. doi:10.1103/PhysRev.104.254. (原始内容 (PDF)存档于2016-03-04) (英语).
- . Nobelprize.org. Nobel Media AB. 2014 [2016-07-07]. (原始内容存档于2016-02-02) (英语).
- Gorter, C. J. . Physica. 1948, 14 (8): 504. Bibcode:1948Phy....14..504G. doi:10.1016/0031-8914(48)90004-4 (英语).
- Rose, M. E. . Physical Review. 1949, 75 (1): 213. Bibcode:1949PhRv...75Q.213R. doi:10.1103/PhysRev.75.213 (英语).
- Ziino, G. (PDF). International Journal of Theoretical Physics. 2006, 45 (11): 1993–2050. Bibcode:2006IJTP...45.1993Z. doi:10.1007/s10773-006-9168-2 (英语).
- Garwin, R. L.; Lederman, L. M.; Weinrich, M. (PDF). Physical Review. 1957, 105 (4): 1415–1417 [2016-07-04]. Bibcode:1957PhRv..105.1415G. doi:10.1103/PhysRev.105.1415. (原始内容存档 (PDF)于2021-04-20) (英语).
- Ambler, E.; Hayward, R. W.; Hoppes, D. D.; Hudson, R. P.; Wu, C. S. (PDF). Physical Review. 1957, 106 (6): 1361–1363 [2016-07-04]. Bibcode:1957PhRv..106.1361A. doi:10.1103/PhysRev.106.1361. (原始内容 (PDF)存档于2013-12-03) (英语).
- Gardner, M. 3rd Revised. Courier Corporation. 2005: 215-218. ISBN 978-0-486-44244-0 (英语).
- Lederman, L. M.; Hill, C. T. . Prometheus Books. 2013: 125-126. ISBN 978-1-61614-802-7 (英语).
- Drewes, M. . International Journal of Modern Physics E. 2013, 22 (8): 1330019. Bibcode:2013IJMPE..2230019D. arXiv:1303.6912
 . doi:10.1142/S0218301313300191 (英语).
. doi:10.1142/S0218301313300191 (英语).
延伸阅读
- Martin, W. C.; Coursey, J.; Dragoset, R. A. . NIST Physical Measurement Laboratory. 1997 [2016-07-04]. (原始内容存档于2016-07-23) (英语).