哈密頓路徑
在圖論中,()是在無向圖或有向圖中,恰好能將圖中所有頂點各拜訪一次的路徑。與之相近的概念為(),即該路徑在拜訪完圖中所有頂點後會回到出發點,而構成一個環。要確定圖中是否存在哈密頓路徑或哈密頓環的問題稱為哈密顿路径问题[1],這個問題是一個NP完全的問題。哈密頓路徑有時會跟尤拉路徑一起討論,因為哈密頓路徑要求通過所有頂點(哈密顿路径问题)而尤拉路徑要求通過所有邊(一筆畫問題)。[2]:218[3]
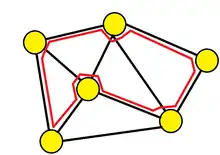
經過圖中所有頂點的迴路稱為哈密頓環
定義
哈密頓路徑是一個拜訪過某圖所有頂點的路徑,且每個頂點只會被拜訪一次。[4]存在哈密頓路徑的圖稱為可追蹤圖。如果一個圖中每對頂點都能找到一條哈密頓路徑,則這個圖可以被視為哈密頓連通的。哈密頓環或哈密頓迴路是一個拜訪過某圖所有頂點的環或循環路徑[5]:196,在這個循環路徑中每個頂點只會被拜訪一次,且拜訪完所有頂點後會回到起始點。存在哈密頓環的圖稱為哈密頓圖[6][7]。哈密頓環與哈密頓路徑主要可以由起點和終點來區別:若一哈密頓路徑起點與終點相同,其為哈密頓環;而若起點與終點不同,則其就不是哈密頓環,僅能視為哈密頓路徑。[8]
哈密頓分解是將圖分解成哈密頓環的邊分解方式。[9]
性質
任何哈密頓環都可以透過移除一條邊來轉換成哈密頓路徑。然而哈密頓路徑只有路徑的2端點相鄰時才有機會透過新增一條邊來轉換成哈密頓環。所有具備哈密頓環的圖(即哈密頓圖)都是雙連通圖;但雙連通圖不一定會存在哈密頓環(即雙連通圖不一定是哈密頓圖,如佩特森圖)。[12]
階數為n(n=1,2,3...)的簡單圖中存在的哈密頓環的總數為0, 0, 2, 10, 58, 616, 9932, 333386, 25153932, 4548577688, ...(OEIS數列A124964)。[13]
參考文獻
- . 資訊與通信術語辭典. 國家教育研究院. 2003年6月 [2021-09-03]. (原始内容存档于2021-09-03).
- (PDF). 興邦二校. [2021-09-03]. (原始内容存档 (PDF)于2021-08-06).
- 徐力行. . 天下文化. 2003-09-16. ISBN 9789864171842 (中文(臺灣)).
- . ck.tp.edu.tw. [2021-09-03]. (原始内容存档于2019-10-30).
- Skiena, Steven; Pemmaraju, Sriram. . . Cambridge University Press. 1990: 196-198. ISBN 978-0521806862.
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . ntnu.edu.tw. [2021-09-03]. (原始内容存档于2021-09-03).
- Bermond, J.-C., , Annals of Discrete Mathematics, 1978, 3: 21–28, ISBN 9780720408430, MR 0505807, doi:10.1016/S0167-5060(08)70494-1
- de Ruiter, Johan. . 2017.
- Friedman, Erich. . Erich's Puzzle Palace. 2009 [27 May 2017]. (原始内容存档于16 April 2016).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2021-09-03]. (原始内容存档于2018-01-15) (英语).
- Sloane, N.J.A. (编). . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.