哥隆尺问题
哥隆尺問題(Golomb ruler),是如何在一把尺上劃分刻度,使所有刻度彼此之間的距離都不相同。刻度的數目稱為階,而兩個刻度間最長的距離為長度。對哥隆尺做平移或鏡像並不影響結果,因此習慣上將最小刻度設為 0 。
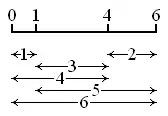
四个刻度长度为6的哥隆尺.这个哥隆尺既是完美的也是最优的。
哥隆尺是由Sidon[1]和Babcock[2]各自独立发现,并且以数学家所羅門·格倫布的名字命名。
哥隆尺不需要能够測量到其自身長度為止的所有距离,如果能夠的话,稱為完美哥隆尺。已經证明不存在五階以上的完美哥隆尺[3]。最優哥隆尺則是同一階中長度最短的哥隆尺。生成哥隆尺是简单的,但是找到一个指定階的最优哥隆尺是的一个有挑战性的计算项目。
Distributed.net(页面存档备份,存于)已经利用大規模分散式平行計算完成了对24階到27階最優哥隆尺的尋找。Distributed.net已於2014年2月開始尋找28階最優哥隆尺。
目前,尋找n階最優哥隆尺的複雜度是未知的,有人猜測這是NP困難問題[3]。
已经发现的最优哥隆尺
下表列出了目前已知的最优哥隆尺。
| 階 | 長度 | 刻度 |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 0 1 |
| 3 | 3 | 0 1 3 |
| 4 | 6 | 0 1 4 6 |
| 5 | 11 | 0 1 4 9 11 0 2 7 8 11 |
| 6 | 17 | 0 1 4 10 12 17 0 1 4 10 15 17 0 1 8 11 13 17 0 1 8 12 14 17 |
| 7 | 25 | 0 1 4 10 18 23 25 0 1 7 11 20 23 25 0 1 11 16 19 23 25 0 2 3 10 16 21 25 0 2 7 13 21 22 25 |
| 8 | 34 | 0 1 4 9 15 22 32 34 |
| 9 | 44 | 0 1 5 12 25 27 35 41 44 |
| 10 | 55 | 0 1 6 10 23 26 34 41 53 55 |
| 11 | 72 | 0 1 4 13 28 33 47 54 64 70 72 0 1 9 19 24 31 52 56 58 69 72 |
| 12 | 85 | 0 2 6 24 29 40 43 55 68 75 76 85 |
| 13 | 106 | 0 2 5 25 37 43 59 70 85 89 98 99 106 |
| 14 | 127 | 0 4 6 20 35 52 59 77 78 86 89 99 122 127 |
| 15 | 151 | 0 4 20 30 57 59 62 76 100 111 123 136 144 145 151 |
| 16 | 177 | 0 1 4 11 26 32 56 68 76 115 117 134 150 163 168 177 |
| 17 | 199 | 0 5 7 17 52 56 67 80 81 100 122 138 159 165 168 191 199 |
| 18 | 216 | 0 2 10 22 53 56 82 83 89 98 130 148 153 167 188 192 205 216 |
| 19 | 246 | 0 1 6 25 32 72 100 108 120 130 153 169 187 190 204 231 233 242 246 |
| 20 | 283 | 0 1 8 11 68 77 94 116 121 156 158 179 194 208 212 228 240 253 259 283 |
| 21 | 333 | 0 2 24 56 77 82 83 95 129 144 179 186 195 255 265 285 293 296 310 329 333 |
| 22 | 356 | 0 1 9 14 43 70 106 122 124 128 159 179 204 223 253 263 270 291 330 341 353 356 |
| 23 | 372 | 0 3 7 17 61 66 91 99 114 159 171 199 200 226 235 246 277 316 329 348 350 366 372 |
| 24 | 425 | 0 9 33 37 38 97 122 129 140 142 152 191 205 208 252 278 286 326 332 353 368 384 403 425 |
| 25 | 480 | 0 12 29 39 72 91 146 157 160 161 166 191 207 214 258 290 316 354 372 394 396 431 459 467 480 |
| 26 | 492 | 0 1 33 83 104 110 124 163 185 200 203 249 251 258 314 318 343 356 386 430 440 456 464 475 487 492 |
| 27 | 553 | 0 3 15 41 66 95 97 106 142 152 220 221 225 242 295 330 338 354 382 388 402 415 486 504 523 546 553 |
| 28 | 585 | 0 3 15 41 66 95 97 106 142 152 220 221 225 242 295 330 338 354 382 388 402 415 486 504 523 546 553 585 |
参考资料
- Sidon, S. . Mathematische Annalen. 1932, 106: 536–539. doi:10.1007/BF01455900.
- Babcock, Wallace C. . Bell System Technical Journal. 1953, 31: 63–73.
- . [2020-05-18]. (原始内容存档于2009-04-20).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.