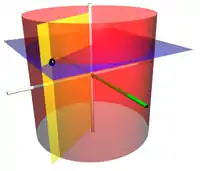
圓柱坐標系
圓柱坐標系(英語:)是一種三維坐標系統。它是二維極坐標系往 z-軸的延伸。添加的第三個坐標 專門用來表示 P 點離 xy-平面的高低。按照國際標準化組織建立的約定 (ISO 31-11) ,徑向距離、方位角、高度,分別標記為 。
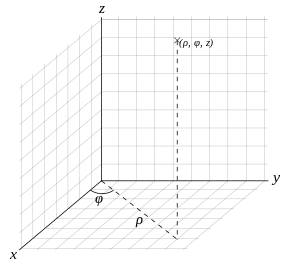
用圓柱坐標 來表示一個點的位置
符號約定
圓柱坐標系的記號並不統一。ISO標準31-11推薦(ρ, φ, z),這裡的ρ是徑向距離,φ是方位角,而z是高度。但是,徑向距離也常表示為r[1]或s,方位角也常表示為θ或t,高度坐標也常表示為h或x(如果圓柱軸被認為是水平的)或任何特定於上下文的字母。
坐標系變換
三維空間裏,有許多各種各樣的坐標系。圓柱坐標系只是其中一種。圓柱坐標系與其他坐標系的變換需要用到特別的方程式。
球坐標系

用球坐標 來表示一個點的位置
使用以下方程式,可以從球坐標變換為圓柱坐標:
- 、
- 、
- 。
相反地, 可以從圓柱坐標變換為球坐標:
- 、
- 、
- 。
圆柱坐标系下的微积分公式
圓柱坐標系的坐標因子分別為
- 、
- 、
- 。

在許多關於圓柱坐標系的問題中,我們時常需要知道線元素與體積元素的方程式;用這些方程式來求解關於徑長或體積的積分問題。線元素是
- 。
面積元素是
- 。
體積元素是
- 。
劈形算符表示為
- 。
- 。
其它微分算子,像 , ,都可以用 坐標表示,只要將標度因子代入在正交坐標系條目內對應的一般公式。
應用
圓柱坐標常被用來分析,選用 z-軸為對稱軸,有軸對稱特性的物體。例如,一個無限長的圓柱,具有直角坐標方程式 ;用圓柱坐標來表示,有一個非常簡易的方程式 。這也是圓柱坐標系名稱的由來。
參考資料
- David K. Cheng. . 2014: 第33頁. ISBN 9781292026565.
參閱
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.