多卷波混沌吸引子

陈氏系统： ${\displaystyle {\frac {\mathrm {d} x(t)}{\mathrm {d} t}}=a*(y(t)-x(t)),}$

${\displaystyle {\frac {\mathrm {d} y(t)}{\mathrm {d} t}}=(c-a)*x(t)-x(t)*f+c*y(t),}$

${\displaystyle {\frac {\mathrm {d} z(t)}{\mathrm {d} t}}=x(t)*y(t)-b*z(t)}$

其中 ${\displaystyle f}$ 为调控函数：[1]

正弦调控函数

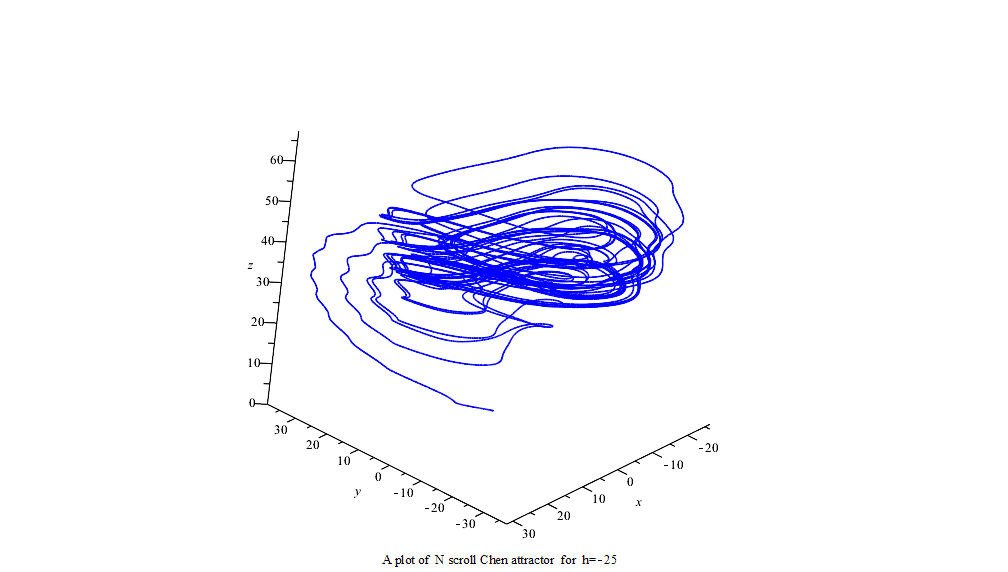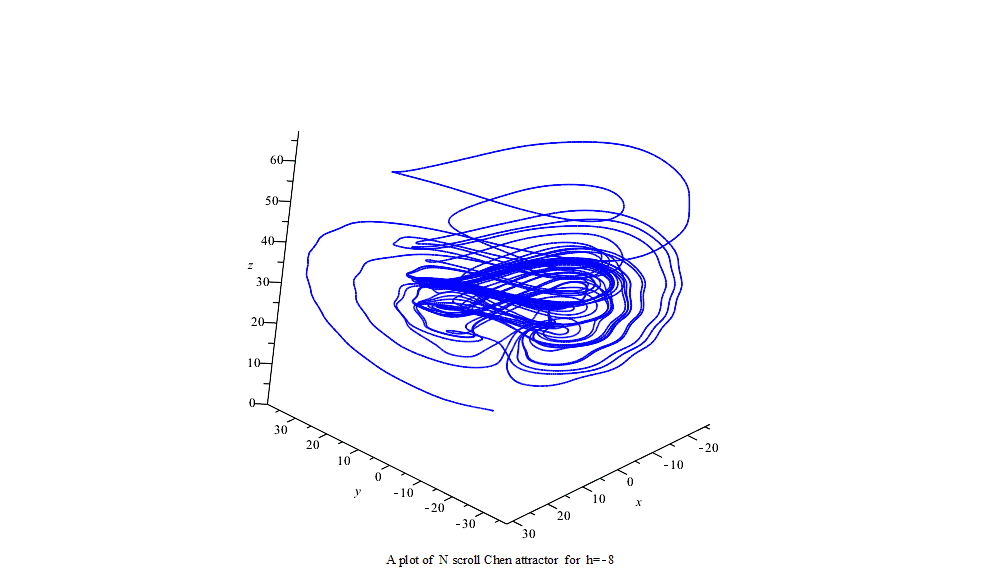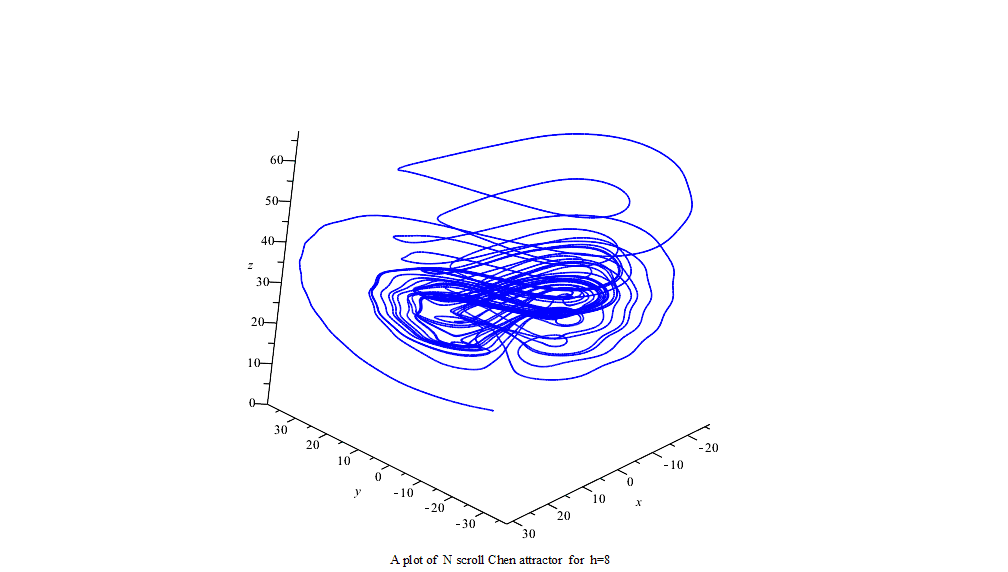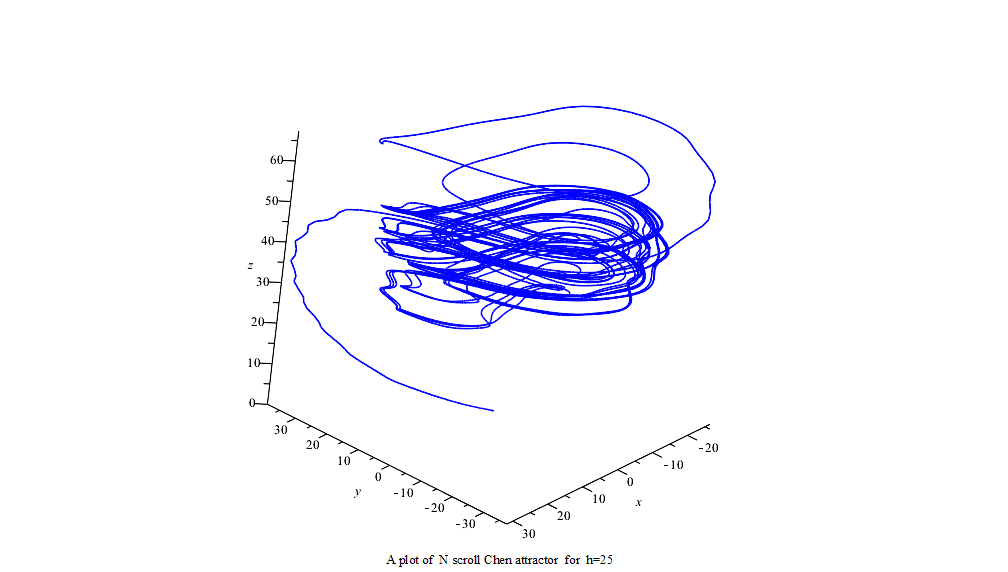
51 frame N scroll modified Chen attractor x axe vs t

${\displaystyle f=g*z(t)-h*\sin(z(t))}$

参数：

:= a = 35, c = 28, b = 3, g = 1, h = -25..25;

初始条件：

initv := x(0) = 1, y(0) = 1, z(0) = 14;

利用Maple中龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg法，简称 RKF45）可得数字解并做图。

h	卷波数
5	4
8	6
22	14

延时正弦函数

N scroll attractor based on Chen with sine and tau

${\displaystyle f=d0*z(t)+d1*z(t-\tau )-d2*\sin(z(t-\tau ))}$

参数：

params := a = 35, c = 28, b = 3, d0 = 1, d1 = 1, d2 = -20..20, tau = .2;

初始条件：

initv := x(0) = 1, y(0) = 1, z(0) = 14;

利用Maple中龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg法，简称 RKF45）可得数字解并做图。

2001年Tang等提出改进的蔡氏吸引子系统：.[2]

${\displaystyle {\frac {\mathrm {d} x(t)}{\mathrm {d} t}}=\alpha *(y(t)-h)}$

${\displaystyle {\frac {\mathrm {d} y(t)}{\mathrm {d} t}}=x(t)-y(t)+z(t)}$

${\displaystyle {\frac {\mathrm {d} z(t)}{\mathrm {d} t}}=-\beta *y(t)}$

其中

${\displaystyle h:=-b*sin({\frac {\pi *x(t)}{2*a}}+d)}$

参数：

params := alpha = 10.82, beta = 14.286, a = 1.3, b = .11, c = 7, d = 0;

初始条件：

initv := x(0) = 1, y(0) = 1, z(0) = 0;

利用Maple中龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg法，简称 RKF45）可得数字解并做图：

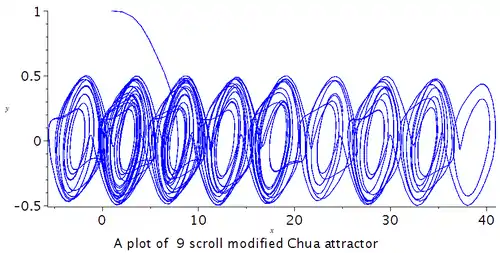
9 卷波 超混沌蔡氏吸引子

9 卷波 超混沌蔡氏吸引子

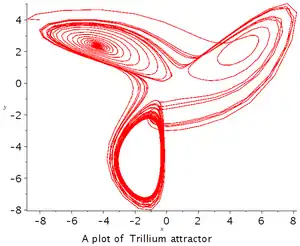
延龄草型混沌吸引子

1993年 Miranda & Stone 提出下列方程组：[3]

${\displaystyle {\frac {\mathrm {d} x(t)}{\mathrm {d} t}}=1/3*(-(a+1)*x(t)+a-c+z(t)*y(t))+((1-a)*(x(t)^{2}-y(t)^{2})+(2*(a+c-z(t)))*x(t)*y(t))}$${\displaystyle *{\frac {1}{3*{\sqrt {x(t)^{2}+y(t)^{2}}}}}}$

${\displaystyle {\frac {\mathrm {d} y(t)}{\mathrm {d} t}}=1/3*((c-a-z(t))*x(t)-(a+1)*y(t))+((2*(a-1))*x(t)*y(t)+(a+c-z(t))*(x(t)^{2}-y(t)^{2}))}$${\displaystyle *{\frac {1}{3*{\sqrt {x(t)^{2}+y(t)^{2}}}}}}$

${\displaystyle {\frac {\mathrm {d} z(t)}{\mathrm {d} t}}=1/2*(3*x(t)^{2}*y(t)-y(t)^{3})-b*z(t)}$

参数：${\displaystyle a=10,\quad b={\frac {8}{3}},\quad c={\frac {137}{5}}}$

初始条件：${\displaystyle x(0)=-8,\quad y(0)=4,\quad z(0)=10}$

利用Maple中龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg法，简称 RKF45）可得数字解并做图：

2000年Aziz Alaoui 提出 PWL Duffing 方程：[4]。

PWL 杜芬方程：

${\displaystyle {\frac {\mathrm {d} x(t)}{\mathrm {d} t}}=y(t)}$

${\displaystyle {\frac {\mathrm {d} y(t)}{\mathrm {d} t}}=-m1*x(t)-(1/2*(m0-m1))*(|x(t)+1|-|x(t)-1|)-e*y(t)+\gamma *cos(\omega *t)}$

参数：

params := e = .25, gamma = .14+(1/20)*i, m0 = -0.845e-1, m1 = .66, omega = 1; c := (.14+(1/20)*i)，i=-25..25;

初始条件：

initv := x(0) = 0, y(0) = 0;

利用Maple中龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg法，简称 RKF45）可得数字解并做图：

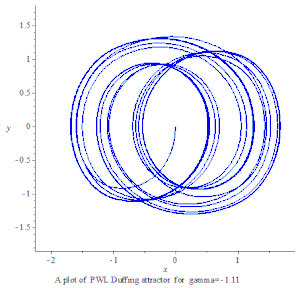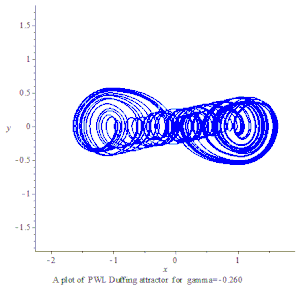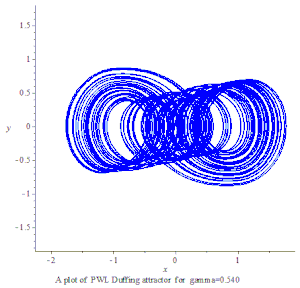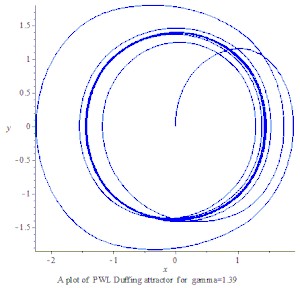
PWL Duffing chaotic attractor xy plot

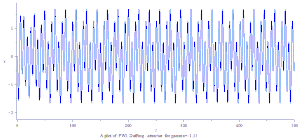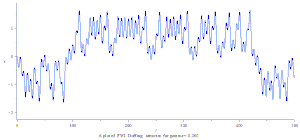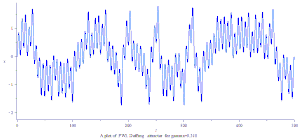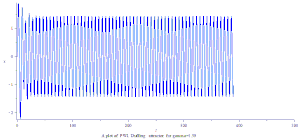
PWL Duffing chaotic attractor plot

• The double-scroll attractor and Chua's circuit （页面存档备份，存于）
• Lozi, R.; Pchelintsev, A.N. . International Journal of Bifurcation and Chaos. 2015, 25 (13): 1550187 [2020-10-08]. doi:10.1142/S0218127415501874. （原始内容存档于2019-05-02）.