大氣邊界層

大气边界层的形成主要是因为地表摩擦力的存在。一方面，近表面的空气分子受摩擦而减慢速度，类似静止，这些分子和流动的分子之间不断交换，总效果是减慢了空气流动。另一方面，更重要的是，在地表附近，空气会形成一系列不规则漩涡，变为湍流，从而对空气流动带来巨大阻力。[2]

湍流是和层流相对的概念。在层流情况下，流体流动的速度和方向相似；但在湍流情况下，不同层之间存在尺度不同的涡旋，且湍流往往具有较强的不稳定性，能使不同层的流体之间互相混合。湍流的存在是大气边界层的重要特征。[1]^:375边界层中的湍流尺度一般较小，在200m左右，表面层湍流尺度则更小，在20m左右。[1]^:376

产生原因

卡门涡街示意图

• 风切变。地面摩擦力对大气运动产生明显影响，因此地面风速相对较小，有时风向也会改变，统称为风切变。
  • 卡门涡街：当大气流动经过小岛等阻流体时，会在其下游产生一系列的交错排列的涡旋。
• 垂直对流。白天地面热空气上升，冷空气下降，产生热力原因的垂直对流。
• 湍流级联。在大涡旋的边缘，由于大气的惯性，会产生较小的涡旋。[1]^:376

通常情况下，由于空气动力学阻力，在距离地球表面仅几百米的地方（行星边界层的表面层），存在着一个风梯度。由于不滑移条件，风速从零[5]开始随离地高度的增加而增大[6]。

近地表风速的减小量是表面粗糙程度的函数，因此具不同地貌特征的地区，风速廓线也不同。[6]粗糙、不规则的地表和地面上的人造建筑可使风速相对于地转风减小40%到50%；[7][8]对于开放水域或冰面，则可能只减少20%到30%。[9][10]这些因素会在选择风力发电机的建造位置时被考虑。[11][12]

在工程学上，人们常常用简单剪切来建模风梯度：假定风速垂直廓线按幂函数变化，并具有常数指数；假定存在一“梯度高度”，在此高度以上地表摩擦对风速影响很小，从而风速为常数，该风速称为“梯度风速”。[8][13][14]例如，对于大城市，预测的梯度高度的典型值是457 m，对于城市郊区来说是366 m，对于空旷地区来说是274 m，对于开放海域来说是213 m。[15]不过，这种近似尽管方便，却并无理论依据。[16]当温度廓线是绝热过程所导致，风速应该与高度成对数关系。[17]1961年在空旷地区进行的一次测量表明，对数拟合在100 m以下（表面层内）吻合良好，且平均风速在1000米高度以上接近恒定。[18]

近地表的障碍物除了降低风速以外，还会向风速引入与其方向垂直的随机的竖直和水平速度分量，使得其风向也与地转风不同。[19]从近地表到高空，风向从紊乱变为均匀，其变化幅度也与地表粗糙程度有关，在开放水域，风向与等压线的夹角约为10°，丘陵地域30°，在陆地当风速非常低时则可达40°-50°。[10]

正如纳维-斯托克斯方程所揭示，大气边界层中的湍流在地表附近的表面层中产生。该层具有最大风速梯度，约占边界层总高度的5％-10%。[1]^:383在表面层之上，湍流逐渐消散，因为湍流动能因摩擦而损失，也有些动能被转化为势能。[1]^:380一些数值模型利用湍流动能产生速率与其耗散速率之间的平衡来计算边界层的高度。[20]

边界层高度差异很大。在陆地，边界层高度存在昼夜变化，白天边界层高度较高，在海洋则无显著昼夜变化。边界层高度也存在地域变化，一般在1~3 km，但有时也可从几十米到4 km或更多[1]^:375，在青藏高原甚至达到5 km或更多。[21]这一变化的原因之一是地面潮湿程度，边界层在植被覆盖的潮湿区域较低，在干燥的地方较高。例如在洋面上边界层高度较低，这是由于水汽的竖直混合使得表面加热效果几乎不存在。[22]边界层高度还存在季节性变化，风暴、地形、城乡等因素也均能影响边界层的高度及形态。[1]^:404[22]

• 
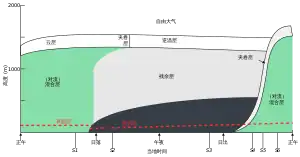
  晴天时不同地表上空大气边界层的位置。红色虚线代表边界层顶。

大气边界层中的湍流导致了非常强的能量和物质交换。由于地面的摩擦作用，大量大气动能在边界层内耗散掉，动能的耗散对大尺度风系统起着刹车的作用。[24]由于强混合作用几乎只存在于边界层内，大气边界层还是许多痕量气体、气溶胶和大气污染物的汇。[25]由于污染物基本存在于边界层内，污染物量相同情况下，边界层高度越低，近地污染物浓度越高。在没有逆温且对流足够强大之时，尤其是在夏季雷雨天气，雷暴会清除污染物，将其带到远在边界层以上的地方。[22]大气边界层的状态还能够影响土壤侵蚀作用。[26]经受热抬升到抬升凝结高度而形成的边界层云的形态能够影响天气和气候，有些海洋区域大多数时候被其覆盖。[1]^:401-402边界层云还起到对阳光的散射作用，这有利于生物圈中的光合作用，使之速率增加。[22]