大Q勒让德多项式

大q-勒让德多项式满足下列正交关系

${\displaystyle \int _{cq}^{q}P_{m}(x;c;q)P_{n}(x;c;q)d_{q}x=q(1-c){\frac {1-q}{1-q^{2n+1}}}{\frac {(c^{-1}q;q)_{n}}{(cq;q)_{n}}}(-cq^{2})^{n}q^{n \choose 2}\delta _{mn}}$

大Q勒让德多项式→勒让德多项式

${\displaystyle \displaystyle \lim _{q\to 1}P_{n}(x;0;q)=P_{n}(2x-1)}$

令大q勒让德项式中的${\displaystyle c=0}$,并且q→1 即得勒让德多项式

验证

将c=0代人7阶(n=7)大q勒让德多项式得：

${\displaystyle qL=P_{n}(x;0;q)=1+{\frac {q}{\left(1-q\right)^{2}}}-{\frac {qx}{\left(1-q\right)^{2}}}-{\frac {{q}^{9}}{\left(1-q\right)^{2}}}+{\frac {x{q}^{9}}{\left(1-q\right)^{2}}}-{\frac {1}{{q}^{6}\left(1-q\right)^{2}}}+{\frac {x}{{q}^{6}\left(1-q\right)^{2}}}+{\frac {{q}^{2}}{\left(1-q\right)^{2}}}-{\frac {x{q}^{2}}{\left(1-q\right)^{2}}}+\left(1-{q}^{-7}\right)\left(1-{q}^{-6}\right)\left(1-{q}^{8}\right)\left(1-{q}^{9}\right)\left(1-x\right)\left(1-qx\right){q}^{2}\left(1-q\right)^{-2}\left(1-{q}^{2}\right)^{-2}+\left(1-{q}^{-7}\right)\left(1-{q}^{-6}\right)\left(1-{q}^{-5}\right)\left(1-{q}^{8}\right)\left(1-{q}^{9}\right)\left(1-{q}^{10}\right)\left(1-x\right)\left(1-qx\right)\left(1-x{q}^{2}\right){q}^{3}\left(1-q\right)^{-2}\left(1-{q}^{2}\right)^{-2}\left(1-{q}^{3}\right)^{-2}+\left(1-{q}^{-7}\right)\left(1-{q}^{-6}\right)\left(1-{q}^{-5}\right)\left(1-{q}^{-4}\right)\left(1-{q}^{8}\right)\left(1-{q}^{9}\right)\left(1-{q}^{10}\right)\left(1-{q}^{11}\right)\left(1-x\right)\left(1-qx\right)\left(1-x{q}^{2}\right)\left(1-x{q}^{3}\right){q}^{4}\left(1-q\right)^{-2}\left(1-{q}^{2}\right)^{-2}\left(1-{q}^{3}\right)^{-2}\left(1-{q}^{4}\right)^{-2}+\left(1-{q}^{-7}\right)\left(1-{q}^{-6}\right)\left(1-{q}^{-5}\right)\left(1-{q}^{-4}\right)\left(1-{q}^{-3}\right)\left(1-{q}^{8}\right)\left(1-{q}^{9}\right)\left(1-{q}^{10}\right)\left(1-{q}^{11}\right)\left(1-{q}^{12}\right)\left(1-x\right)\left(1-qx\right)\left(1-x{q}^{2}\right)\left(1-x{q}^{3}\right)\left(1-x{q}^{4}\right){q}^{5}\left(1-q\right)^{-2}\left(1-{q}^{2}\right)^{-2}\left(1-{q}^{3}\right)^{-2}\left(1-{q}^{4}\right)^{-2}\left(1-{q}^{5}\right)^{-2}+\left(1-{q}^{-7}\right)\left(1-{q}^{-6}\right)\left(1-{q}^{-5}\right)\left(1-{q}^{-4}\right)\left(1-{q}^{-3}\right)\left(1-{q}^{-2}\right)\left(1-{q}^{8}\right)\left(1-{q}^{9}\right)\left(1-{q}^{10}\right)\left(1-{q}^{11}\right)\left(1-{q}^{12}\right)\left(1-{q}^{13}\right)\left(1-x\right)\left(1-qx\right)\left(1-x{q}^{2}\right)\left(1-x{q}^{3}\right)\left(1-x{q}^{4}\right)\left(1-x{q}^{5}\right){q}^{6}\left(1-q\right)^{-2}\left(1-{q}^{2}\right)^{-2}\left(1-{q}^{3}\right)^{-2}\left(1-{q}^{4}\right)^{-2}\left(1-{q}^{5}\right)^{-2}\left(1-{q}^{6}\right)^{-2}+\left(1-{q}^{-7}\right)\left(1-{q}^{-6}\right)\left(1-{q}^{-5}\right)\left(1-{q}^{-4}\right)\left(1-{q}^{-3}\right)\left(1-{q}^{-2}\right)\left(1-{q}^{-1}\right)\left(1-{q}^{8}\right)\left(1-{q}^{9}\right)\left(1-{q}^{10}\right)\left(1-{q}^{11}\right)\left(1-{q}^{12}\right)\left(1-{q}^{13}\right)\left(1-{q}^{14}\right)\left(1-x\right)\left(1-qx\right)\left(1-x{q}^{2}\right)\left(1-x{q}^{3}\right)\left(1-x{q}^{4}\right)\left(1-x{q}^{5}\right)\left(1-x{q}^{6}\right){q}^{7}\left(1-q\right)^{-2}\left(1-{q}^{2}\right)^{-2}\left(1-{q}^{3}\right)^{-2}\left(1-{q}^{4}\right)^{-2}\left(1-{q}^{5}\right)^{-2}\left(1-{q}^{6}\right)^{-2}\left(1-{q}^{7}\right)^{-2}}$

• ${\displaystyle qL2=\lim _{q\to 1}qL=-1+56\,x+3432\,{x}^{7}-12012\,{x}^{6}+16632\,{x}^{5}-11550\,{x}^{4}+4200\,{x}^{3}-756\,{x}^{2}}$

另7阶勒让德多项式：

• ${\displaystyle P_{7}(2x-1)=-1+56\,x+3432\,{x}^{7}-12012\,{x}^{6}+16632\,{x}^{5}-11550\,{x}^{4}+4200\,{x}^{3}-756\,{x}^{2}}$

显然qL2=P_7(2x-1) QED.

下列复数域三阶大q勒让德多项式:${\displaystyle \displaystyle P_{n}3(x+iy;-1.5;q)}$的

一组三个虚数部、实数部与绝对值的复数三维动画图，以q为可变参数

一组三个虚数部、实数部与绝对值的复数密度动画图

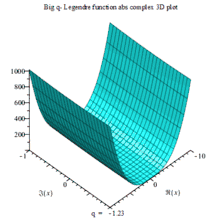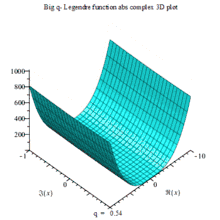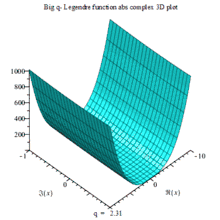BIG Q-LEGENDER ABS COMPLEX 3D MAPLE PLOT

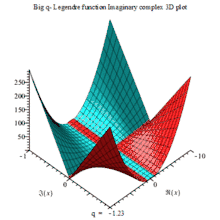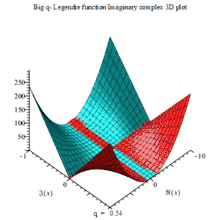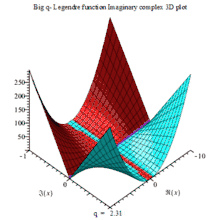BIG Q-LEGENDER IM COMPLEX 3D MAPLE PLOT

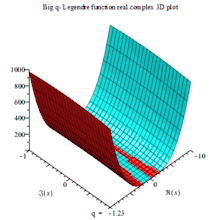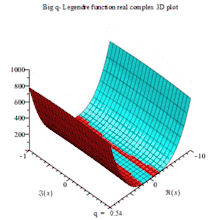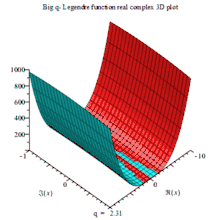BIG Q-LEGENDER RE COMPLEX 3D MAPLE PLOT

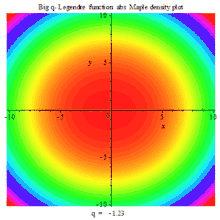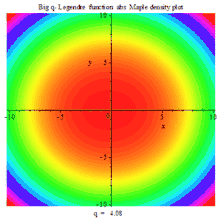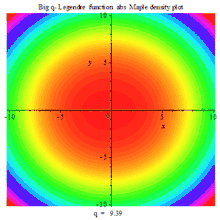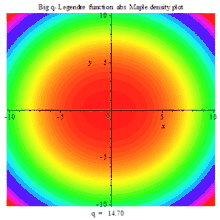BIG Q-LEGENDER ABS DENSITY MAPLE PLOT

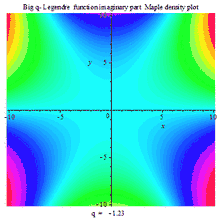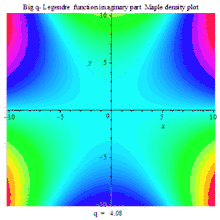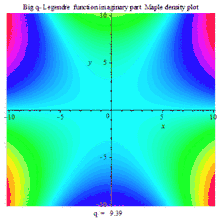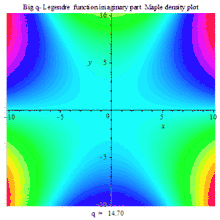BIG Q-LEGENDER IM DENSITY MAPLE PLOT

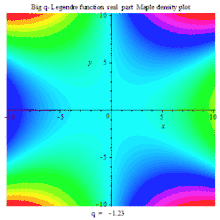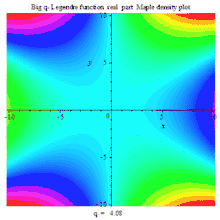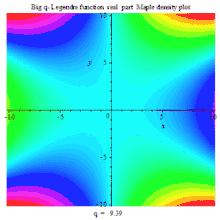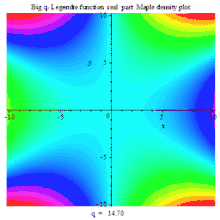BIG Q-LEGENDER RE DENSITY MAPLE PLOT

• Andrews, George E.; Askey, Richard, , Brezinski, C.; Draux, A.; Magnus, Alphonse P.; Maroni, Pascal; Ronveaux, A. (编), , Lecture Notes in Math. 1171, Berlin, New York: Springer-Verlag: 36–62, 1985, ISBN 978-3-540-16059-5, MR 0838970, doi:10.1007/BFb0076530
• Gasper, George; Rahman, Mizan, , Encyclopedia of Mathematics and its Applications 96 2nd, Cambridge University Press, 2004, ISBN 978-0-521-83357-8, MR 2128719, doi:10.2277/0521833574
• Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F., , Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, 2010, ISBN 978-3-642-05013-8, MR 2656096, doi:10.1007/978-3-642-05014-5
• Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F., http://dlmf.nist.gov/18 |contribution-url=缺少标题 (帮助), Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (编), , Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248

1. Roelof p443