奇异边界法

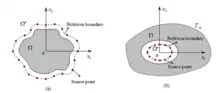
奇异边界法最初于2009年[6]提出。该方法使用基本解作为插值基函数，并直接将插值源点布置在问题的真实边界上，克服了传统基本解方法中最复杂最头疼的虚拟边界问题。为避免配置点与插值源点重合时带来的基本解源点奇异性，该方法首次提出了源点强度因子的概念，从而将边界型强格式方法的核心归结为求解源点强度因子。目前，该方法已成功应用于求解位势问题[7][8]、无限域问题[9]、弹性力学问题[10]等。

目前发展了两种方法来计算源点强度因子。第一种方法采用一种反插值的数值处理技术间接求解源点强度因子。该方法首先需要在物理域内布置一组与边界源点不重合的内部点(称之为样本点)，然后通过求解一个代数方程组来间接计算源点强度因子；第二种方法基于边界元法中处理奇异积分的技术与方法，直接导出了源点强度因子的解析表达式[11]。数值算例表明，第二种方法更为稳定，精度更高。

当配置点接近但又不在边界单元时，配置点与源点的距离不等于零但又十分趋近于零。从数学的意义上，基本解此时是非奇异的。但是从计算的角度讲，当配置点接近边界时，基本解表现出剧烈的震荡特性，产生所谓的“几乎奇异性”，反应了边界型方法中的边界层效应（Boundary layer effect）问题[12]。

针对奇异边界法中的边界层效应问题，文[13]采用一类非线性变量替换法，有效地改善了近边界点基本解的震荡特性，消除了基本解的几乎奇异性。在不增加计算量的情况下，极大地改进了几乎奇异核函数的计算精度，成功求解了近边界点上的力学参量，克服了边界层效应问题。数值试验结果表明，即使配置点和边界的距离达到1.0E-10的数量级，依然能取得理想的数值结果。

同基本解法和边界元法类似，奇异边界法形成的系数矩阵通常是非对称的稠密矩阵。如果边界总的自由度是N的量级，计算和存储这样的系数矩阵则需要O(N²) 的量级，使得常规求解技术效率较低。快速多极算法能将计算量和存储量都降至O(NlogN)甚至O(N)。从而使奇异边界法快速、准确的求解大规模复杂工程问题成为可能。