Talbot曲线
Talbot曲线也稱為切恩豪斯立方曲線,為一平面曲線,極坐標方程式如下
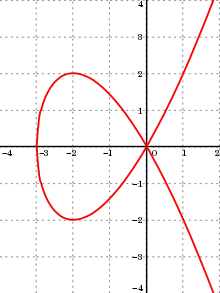
Tschirnhausen立方曲線
歷史
埃伦弗里德·瓦尔特·冯·切恩豪斯、紀堯姆·德·洛必達及歐仁·查爾斯·加泰羅尼亞都曾研究此曲線。在R C Archibald於1900年發表的論文中將此稱為切恩豪斯立方曲線,不過也稱為洛必達立方曲線(de L'Hôpital's cubic)或加泰羅尼亞三等分角线(trisectrix of Catalan)。
參考資料
- J. D. Lawrence, A Catalog of Special Plane Curves. New York: Dover, 1972, pp. 87-90.
外部連結
- 埃里克·韦斯坦因. . MathWorld.
- "Tschirnhaus' Cubic" at MacTutor History of Mathematics Archive(页面存档备份,存于)
- "Cubique de Tschirnhausen" at Encyclopédie des Formes Mathématiques Remarquables(页面存档备份,存于) (in French)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.