安斯库姆四重奏
安斯库姆四重奏()是四组基本的统计特性一致的数据,但由它们绘制出的图表则截然不同。每一组数据都包括了11个(x,y)点。这四组数据由统计学家弗朗西斯·安斯库姆(Francis Anscombe)于1973年构造,他的目的是用来说明在分析数据前先绘制图表的重要性,以及离群值对统计的影响之大。
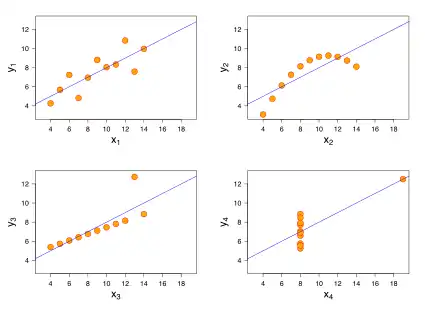
安斯库姆四重奏的四组数据图表
这四组数据的共同统计特性如下:
| 性质 | 数值 |
|---|---|
| x的平均数 | 9 |
| x的方差 | 11 |
| y的平均数 | 7.50(精确到小数点后两位) |
| y的方差 | 4.122或4.127(精确到小数点后三位) |
| x与y之间的相关系数 | 0.816(精确到小数点后三位) |
| 线性回归线 | (分别精确到小数点后两位和三位) |
在四幅图中,由第一组数据绘制的图表(左上图)是看起来最“正常”的,可以看出两个随机变量之间的相关性。从第二组数据的图表(右上图)则可以明显地看出两个随机变量间的关系是非线性的。第三组中(左下图),虽然存在着线性关系,但由于一个离群值的存在,改变了线性回归线,也使得相关系数从1降至0.81。最后,在第四个例子中(右下图),尽管两个随机变量间没有线性关系,但仅仅由于一个离群值的存在就使得相关系数变得很高。
爱德华·塔夫特(Edward Tufte)在他所著的《图表设计的现代主义革命》(The Visual Display of Quantitative Information)一书的第一页中,就使用安斯库姆四重奏来说明绘制数据图表的重要性。
四组数据的具体取值如下所示。其中前三组数据的x值都相同。
| 一 | 二 | 三 | 四 | ||||
|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | x | y |
| 10.0 | 8.04 | 10.0 | 9.14 | 10.0 | 7.46 | 8.0 | 6.58 |
| 8.0 | 6.95 | 8.0 | 8.14 | 8.0 | 6.77 | 8.0 | 5.76 |
| 13.0 | 7.58 | 13.0 | 8.74 | 13.0 | 12.74 | 8.0 | 7.71 |
| 9.0 | 8.81 | 9.0 | 8.77 | 9.0 | 7.11 | 8.0 | 8.84 |
| 11.0 | 8.33 | 11.0 | 9.26 | 11.0 | 7.81 | 8.0 | 8.47 |
| 14.0 | 9.96 | 14.0 | 8.10 | 14.0 | 8.84 | 8.0 | 7.04 |
| 6.0 | 7.24 | 6.0 | 6.13 | 6.0 | 6.08 | 8.0 | 5.25 |
| 4.0 | 4.26 | 4.0 | 3.10 | 4.0 | 5.39 | 19.0 | 12.50 |
| 12.0 | 10.84 | 12.0 | 9.13 | 12.0 | 8.15 | 8.0 | 5.56 |
| 7.0 | 4.82 | 7.0 | 7.26 | 7.0 | 6.42 | 8.0 | 7.91 |
| 5.0 | 5.68 | 5.0 | 4.74 | 5.0 | 5.73 | 8.0 | 6.89 |
参见
参考文献
- F.J. Anscombe, "Graphs in Statistical Analysis," American Statistician, 27 (February 1973), 17-21.
- Tufte, Edward R. (2001). The Visual Display of Quantitative Information, 2nd Edition, Cheshire, CT: Graphics Press. ISBN 0961392142
- Sangit Chatterjee and Aykut Firat (2007). "Generating Data with Identical Statistics but Dissimilar Graphics: A Follow up to the Anscombe Dataset", American Statistician, 61(3), 248-254. doi:10.1198/000313007X220057
外部链接
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.