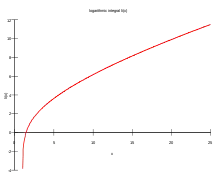
对数积分

对数积分有一个积分的表示法，对所有的正实数${\displaystyle x\neq 1}$都有定义：

${\displaystyle \operatorname {li} (x)=\int _{0}^{x}{\frac {dt}{\ln(t)}}}$

在这里，ln表示自然对数。函数1/ln (t)在t = 1处有一个奇点，当x > 1时，这个积分只能用柯西主值的概念来解释：

${\displaystyle \operatorname {li} (x)=\lim _{\varepsilon \to 0}\left(\int _{0}^{1-\varepsilon }{\frac {dt}{\ln(t)}}+\int _{1+\varepsilon }^{x}{\frac {dt}{\ln(t)}}\right)}$

由於這個積分在x趨近於1時，值會趨近於負無窮大，有些數學家為了避免麻煩，常會選擇另外一個相似的定義，欧拉对数积分定义为：

${\displaystyle \operatorname {Li} (x)=\operatorname {li} (x)-\operatorname {li} (2)}$

或

${\displaystyle \operatorname {Li} (x)=\int _{2}^{x}{\frac {dt}{\ln t}}}$

函数li(x)有一個正根，它出现在x ≈ 1.45136 92348 ...。这个数称为Ramanujan-Soldner常数。

${\displaystyle \operatorname {li} (2)=-(\Gamma \left(0,-\ln 2\right)+i\,\pi )\sim 1.045163780117492784844588889194613136522615578151}$

其中${\displaystyle \Gamma \left(a,x\right)}$是不完全伽玛函数。

函数li(x)与指数积分Ei(x)有以下的关系：

${\displaystyle {\hbox{li}}(x)={\hbox{Ei}}(\ln(x))}$

其中${\displaystyle x>1}$。这个等式提供了li(x)的一个级数表示法：

${\displaystyle \operatorname {li} (e^{u})={\hbox{Ei}}(u)=\gamma +\ln u+\sum _{n=1}^{\infty }{u^{n} \over n\cdot n!}\quad {\text{for }}u\neq 0}$

其中γ ≈ 0.57721 56649 01532 ...是欧拉-马歇罗尼常数。一个收敛得更快的级数，是：

${\displaystyle \operatorname {li} (x)=\gamma +\ln \ln x+{\sqrt {x}}\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}(\ln x)^{n}}{n!\;2^{n-1}}}\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {1}{2k+1}}}$

当x → ∞，函数有以下的渐进表现：

${\displaystyle \operatorname {li} (x)={\mathcal {O}}\left({x \over \ln(x)}\right)}$

其中${\displaystyle {\mathcal {O}}}$是大O符号。完整的渐近展开式为：

${\displaystyle \operatorname {li} (x)={\frac {x}{\ln x}}\sum _{k=0}^{\infty }{\frac {k!}{(\ln x)^{k}}}}$

或

${\displaystyle {\frac {\operatorname {li} (x)}{x/\ln x}}=1+{\frac {1}{\ln x}}+{\frac {2}{(\ln x)^{2}}}+{\frac {6}{(\ln x)^{3}}}+\cdots }$

注意，作为渐近展开式，这个级数是发散的：只有级数前面有限个项才是较好的估计。这个展开式可从指数积分的渐近展开式直接推出。

对数积分在数论中十分重要，出现在小于某个整数的素数个数的估计中。例如，質數定理表明：

${\displaystyle \pi (x)\sim \operatorname {Li} (x)}$

其中π(x)是小于或等于x的素数的个数。

• 指数积分
• 三角积分

• Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 5) （页面存档备份，存于）