對撞因子

對撞因子（英語：），有時又稱為反向分叉（英語：），[1]在統計學和圖模式中，是指同時被兩個以上的變數影響的變數，而這些影響對撞因子的變數之間不見得有因果關係。因為在環路圖上會顯示為有兩個以上箭頭指入的節點，所以稱為對撞因子。[2]

干擾因子、中介因子、對撞因子示意圖

對撞因子不會直接造成影響它的變數之間出現相關，以路徑分析或環路圖的術語來說，對撞因子會「阻斷」兩個變數間的路徑。然而，想要了解變數間的因果關係時，對撞因子非常重要，因為在設計實驗、挑選樣本或統計分析時，如果有意或無意間控制了對撞因子，會造成自變數（X）和應變數（Y）之間出現沒有實際因果關係的偽關係，稱為選擇偏誤或伯克森悖論，如果控制對撞因子後造成相反的相關性，稱為辛普森悖論。用環路圖的術語來說，控制對撞因子會「開啟」 X 和 Y 之間的路徑，而造成偏誤。[3][4][5]

和其他因子的分別

對撞因子有時會和其他因子混淆。

干擾因子同時影響自變數和應變數，在環路圖上顯示為分叉向外的箭頭。干擾因子應該要控制。[6]

中介變項受自變數影響，並影響應變數，在環路圖上箭頭一進一出。如果要研究的問題是「X是否會影響Y」，則不應控制。如果研究的問題是「X是否能夠直接影響Y」，則需要控制。[6]

例子
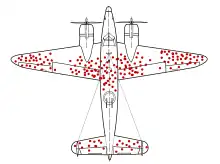
这是安全返回的飞机受损的部分示意图；而其他地方受到攻击的飞机却无法安全返回。(图片为假定的数据)

在二次世界大戰期間，沃德·亞伯拉罕發現盟軍飛回來的飛機中，機翼上有最多彈痕，機尾和引擎最少。他提議補強最少彈痕的地方，而不是中彈最多的地方。因為這些飛機可以飛回來，表示中彈的位置不重要，其他位置中彈的飛機都沒能飛回來，所以才沒有觀察到那些位置中彈。「有彈痕的位置」和「重要的位置」是兩個變因，「是否被擊落」是對撞因子，因為「沒被擊落」的條件已經自動被控制了，所以變因之間出現負相關。這種現象稱作倖存者偏差，在臨床醫學研究中是重要的偏誤：如果只看在醫院裡的病人、或是沒死的病人，容易得出錯誤的結論。[7]

再以籃球為例，如果只看 NBA 球員，會發現身高比較高的人得分率沒有比較高。這是因為身高矮還能進 NBA 的人必然是用其他優勢補足了身高的弱勢。「身高」為自變數，「籃球得分率」為應變數，「是 NBA 球員」是對撞因子。

其他可能的例子：

  • 在網路上傳播的文章，「標題吸引人」和「內容嚴謹」常常是負相關。
  • 維基百科條目中，若是有小眾關注者的主題，品質較差，可能是因為「條目品質佳」和「有人想要寫」都造成「條目存在」。
  • 如果在控制教育程度後，智商和盡責性呈負相關，可能是因為兩者都有助於提升學歷。[8]
  • 如果在控制職業後，兩性的收入相等，這不見得能夠證明女性未受歧視，也可能是因為只有競爭力較佳的少數女性才有辦法在歧視較嚴重的行業中存活，更高的競爭力補足了歧視的影響。[9]

參阅

參考資料
  1. . [2019-05-22]. （原始内容存档于2020-11-20）.
  2. Hernan, Miguel A; Robins, James M, , Chapman & Hall/CRC monographs on statistics & applied probability, CRC: 70, 2010, ISBN 978-1-4200-7616-5
  3. Greenland, Sander; Pearl, Judea; Robins, James M, (PDF), Epidemiology, January 1999, 10 (1): 37–48 [2019-05-22], ISSN 1044-3983, OCLC 484244020, PMID 9888278, doi:10.1097/00001648-199901000-00008, （原始内容存档 (PDF)于2016-03-03）
  4. Pearl, Judea. . Artificial Intelligence. 1986, 29 (3): 241–288. doi:10.1016/0004-3702(86)90072-x.
  5. Pearl, Judea. . Morgan Kaufmann. 1988.
  6. Pearl, Judea; Dana Mackenzie. . 2018: 111-114. ISBN 9780465097609.
  7. Mangel, M. and Samaniego, F. . Journal ofthe American Statistical Association. 1984, 79: 259–267.
  8. Asendorpf JB, Rindermann H, Woodley MA, Stratford J, Rabaglia C, Marcus G, Lane S. (PDF). European Journal of Personality. 2012, 26: 391-413 [2020-02-03]. （原始内容存档 (PDF)于2017-07-25）.
  9. Cunningham, Scott. (PDF). 2018: 74-78 [2019-05-22]. （原始内容 (PDF)存档于2020-12-13）.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.