布豐投針問題
布豐投針問題(,又译“蒲丰投針問題”)是布丰於18世紀提出的一個数学問題:[1]
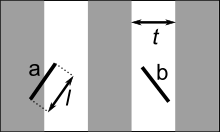
設我們有一個以平行且等距木紋舖成的地板(如右圖),現在隨意拋一支長度比木紋之間距離小的針,求針和其中一條木紋相交的機率。
解法
設針的長度是,平行線之間的距離為,為針的中心和最近的平行線的距離,為針和線之間的銳角。
且均匀分布,其機率密度函數為。
且均匀分布,其機率密度函數為。
兩個隨機變數互相獨立,因此兩者結合的機率密度函數只是兩者的積:
當,針和線相交,然後對積分得出所求機率。
要求上式的積分需要分為兩種情況:“短針”以及“長針”;以下考慮“短針”情況,計算上式積分得針與線相交的機率:
作簡單變換可得,
當拋支針,其中有支針與線相交,利用多次重複試驗所觀察事件發生的頻率越來越接近機率的理論值。
近似可得
拉扎里尼的估計
1901年,意大利數學家马里奥·拉扎里尼(Mario Lazzarini)嘗試進行此實驗。他拋了3408次針,得到π的近似值為355/113。
拉扎里尼選取了一支長度是紋的距離的5/6的針。在這個情況,針和紋相交的機會是5/(3π)。如果想拋n次針而得到x次相交,π約等於。分母、分子少於五位數字,沒有比355/113更好的π的近似值了。因此,可以列式,得。
為求x的值接近這個數,可以重覆拋213次針,若有113次是成功的,便可終止實驗,宣布這個方法求π值準確度不低;否則,就再拋213次針,希望共有226次成功……這次反覆進行實驗。拉扎里尼做了次。
參考文獻
- Histoire de l'Acad. Roy. des. Sciences (1733), 43–45; Histoire naturelle, générale et particulière Supplément 4 (1777), p. 46.
- Behrends, Ehrhard. (PDF). [14 March 2015]. (原始内容存档 (PDF)于2014-08-02).
外部連結
| 维基共享资源中相关的多媒体资源:布豐投針問題 |
- Buffon's Needle Problem (页面存档备份,存于) at cut-the-knot
- Math Surprises: Buffon's Noodle (页面存档备份,存于) at cut-the-knot
- MSTE: Buffon's Needle (页面存档备份,存于)
- Buffon's Needle Java Applet (页面存档备份,存于)
- Estimating PI Visualization (Flash) (页面存档备份,存于)
- Buffon's needle: fun and fundamentals (presentation) (页面存档备份,存于) at slideshare
- Animations for the Simulation of Buffon's Needle (页面存档备份,存于) by Yihui Xie using the R package animation
- 3D Physical Animation (页面存档备份,存于) by Jeffrey Ventrella
- Padilla, Tony. . Numberphile. Brady Haran. [2013-04-09]. (原始内容存档于2013-05-17).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.