帕斯卡蜗线

丢勒所画出的蜗线

数学家布莱兹·帕斯卡的父亲，艾蒂安·帕斯卡（Étienne Pascal）也是一位数学爱好者，他曾于1637年在一封信中提到了自己对蜗线的研究。吉尔·罗伯瓦（Gilles de Roberval）曾用蜗线求过曲线的切线，和三等分角，他将该曲线称之为帕斯卡蜗线。科学史研究者认为艾蒂安·帕斯卡之前一百余年的德国画家阿尔布雷希特·丢勒就曾对这一曲线进行过研究，在他1525年出版的《量度艺术教程》一书中，丢勒给出了蜗线的画法。

以定点O为极点，则帕斯卡蜗线的极坐标方程如下：

${\displaystyle r=b+a\cos \theta \ .}$

其中${\displaystyle a}$为给定圆的直径，${\displaystyle b}$为Q点向两侧所截取的定长。

通过极坐标系和直角坐标系的转换关系，可得到平面直角坐标系下的方程：

${\displaystyle (x^{2}+y^{2}-ax)^{2}=b^{2}(x^{2}+y^{2}).\,}$[1]

需注意此时的方程是以定点O为原点的，若以给定圆的圆心为原点，则方程不同。

如果使用参数方程表示：

${\displaystyle x={a \over 2}+b\cos \theta +{a \over 2}\cos 2\theta ,\,y=b\sin \theta +{a \over 2}\sin 2\theta .}$

可以转换为在复平面里的表达式：

${\displaystyle z={a \over 2}+be^{i\theta }+{a \over 2}e^{2i\theta }.}$

三种帕斯卡蜗线

• ${\displaystyle {\frac {a}{b}}<1}$：蜗线没有绕扣和尖点。
• ${\displaystyle {\frac {a}{b}}=1}$：蜗线带有尖点，此时方程变为：
  • ${\displaystyle r=b(1+\cos \theta )=2b\cos ^{2}{\theta \over 2}}$ or ${\displaystyle r^{1 \over 2}=(2b)^{1 \over 2}\cos {\theta \over 2}}$，即心脏线。
• ${\displaystyle {\frac {a}{b}}>1}$：蜗线带有绕扣，形成内外两圈。
• ${\displaystyle {\frac {a}{b}}=2}$：此时方程变为：
  • ${\displaystyle r=b(1+2\cos \theta )}$, 通过适当的平移之后可以得到
  • ${\displaystyle r=2b\cos {\theta \over 3}}$

这属于玫瑰线一类，被称为帕斯卡三等分角线（Limaçon trisectrix）。

• ${\displaystyle {\frac {a}{b}}>>1}$: 随着${\displaystyle {\frac {a}{b}}}$的值的进一步增大，帕斯卡蜗线的内圈和外圈逐渐接近，趋向于同一个圆。

帕斯卡蜗线所围的面积为${\displaystyle (b^{2}+{{a^{2}} \over 2})\pi }$，但要注意当${\displaystyle b<a}$ 此处的面积为外圈所围的面积${\displaystyle (b^{2}+{{a^{2}} \over 2})(\pi -\arccos {b \over a})+{3 \over 2}b{\sqrt {{a^{2}}-{b^{2}}}}}$+内圈所围的面积${\displaystyle (b^{2}+{{a^{2}} \over 2})\arccos {b \over a}-{3 \over 2}b{\sqrt {{a^{2}}-{b^{2}}}}}$，或者可以认为是两圈之间的面积${\displaystyle (b^{2}+{{a^{2}} \over 2})(\pi -2\arccos {b \over a})+3b{\sqrt {{a^{2}}-{b^{2}}}}.}$+两倍的内圈面积所得。

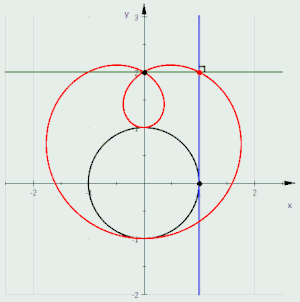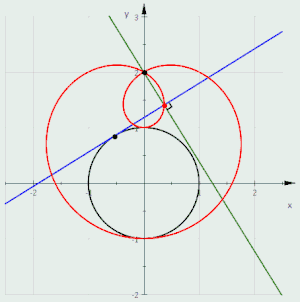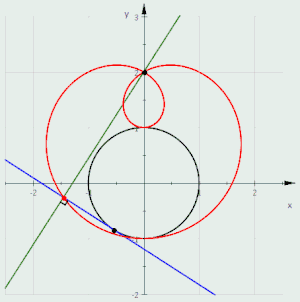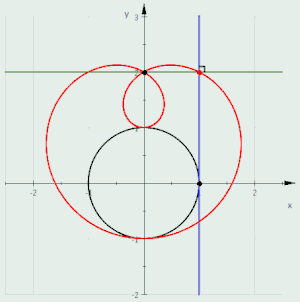
帕斯卡蜗线是圆的垂足曲线的演示

• 若平面上有两个点O和P，则以O为圆心，且过P点的所有圆的包络线是帕斯卡蜗线。

• 若给定一个圆和一点P，则从P点向圆的任何一条切线所作垂线的垂足形成的垂足曲线是帕斯卡蜗线。

• 圆锥曲线的反演变换结果是帕斯卡蜗线，三种不同的圆锥曲线正好对应帕斯卡蜗线的三种情况：
  • 抛物线反演后为具有绕扣的蜗线
  • 双曲线反演后为心脏线
  • 椭圆反演后为没有尖点和绕扣的蜗线。

• 帕斯卡蜗线可以看作是笛卡尔卵形线的特例。[2]
• 一个内壁是球面的反射体的回光线（光线照在内壁上反射线的包络线）是帕斯卡蜗线[3]。

1. J. Dennis Lawrence. . Dover Publications. 1972: 113–118. ISBN 0-486-60288-5.
2. 約翰·J·奧康納; 埃德蒙·F·羅伯遜, , （英语）
3. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2013-06-09]. （原始内容存档于2020-03-19） （英语）.

• Jane Grossman and Michael Grossman. "Dimple or no dimple" （页面存档备份，存于）, The Two-Year College Mathematics Journal, January 1982, pages 52–55.
• Howard Anton. Calculus, 2nd edition, page 708, John Wiley & Sons, 1984.
• Howard Anton. （页面存档备份，存于） pp. 725 – 726.
• Howard Eves. A Survey of Geometry, Volume 2 (pages 51,56,273), Allyn and Bacon, 1965.

维基共享资源上的相关多媒体资源：帕斯卡蜗线

• 埃里克·韦斯坦因. . MathWorld. （页面存档备份，存于）
• "Limacon of Pascal" at The MacTutor History of Mathematics archive （页面存档备份，存于）
• "Limaçon" at www.2dcurves.com （页面存档备份，存于）
• "Limaçons de Pascal" at Encyclopédie des Formes Mathématiques Remarquables （页面存档备份，存于） (in French)
• "Limacon of Pascal" at Visual Dictionary of Special Plane Curves （页面存档备份，存于）
• "Limacon of Pascal" on PlanetPTC (Mathcad)