帕累托分布

帕累托分布(Pareto distribution)是以意大利经济学家维尔弗雷多·帕累托命名的。 是从大量真实世界的现象中发现的幂定律分布。这个分布在经济学以外，也被称为布拉德福分布。

帕累托分布

密度函數
累積分布函數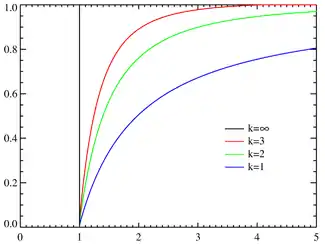
	xm > 0 k > 0
值域	${\displaystyle x\in [x_{\mathrm {m} };+\infty )\!}$
	${\displaystyle {\frac {k\,x_{\mathrm {m} }^{k}}{x^{k+1}}}\!}$
累積分布函數	${\displaystyle 1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{k}\!}$
期望值	${\displaystyle {\frac {k\,x_{\mathrm {m} }}{k-1}}\!}$，${\displaystyle k>1}$
中位數	${\displaystyle x_{\mathrm {m} }{\sqrt[{k}]{2}}}$
眾數	${\displaystyle x_{\mathrm {m} }\,}$
	${\displaystyle {\frac {x_{\mathrm {m} }^{2}k}{(k-1)^{2}(k-2)}}\!}$，${\displaystyle k>2}$
偏度	${\displaystyle {\frac {2(1+k)}{k-3}}\,{\sqrt {\frac {k-2}{k}}}\!}$，${\displaystyle k>3}$
峰度	${\displaystyle {\frac {6(k^{3}+k^{2}-6k-2)}{k(k-3)(k-4)}}\!}$，${\displaystyle k>4}$
熵	${\displaystyle \ln \left({\frac {k}{x_{\mathrm {m} }}}\right)-{\frac {1}{k}}-1\!}$
	未定义
特徵函数	${\displaystyle k(-ix_{\mathrm {m} }t)^{k}\Gamma (-k,-ix_{\mathrm {m} }t)\,}$

在帕累托分布中，如果X是一个随机变量， 则X的概率分布如下面的公式所示：

${\displaystyle {\rm {P}}(X>x)=\left({\frac {x}{x_{\min }}}\right)^{-k}}$

其中x是任何一个大于x_min的数，x_min是X最小的可能值（正数），k是为正的参数。帕累托分布曲线族是由两个数量参数化的：x_min和k。分布密度则为

${\displaystyle p(x)=\left\{{\begin{matrix}0,&{\mbox{if }}x<x_{\min };\\\\{k\;x_{\min }^{k} \over x^{k+1}},&{\mbox{if }}x>x_{\min }.\end{matrix}}\right.}$

帕累托分布属于连续概率分布。 “齊夫定律”, 也称为“zeta 分布”, 也可以被认为是在离散概率分布中的帕累托分布。 一个遵守帕累托分布的随机变量的期望值为 ${\displaystyle x_{\min }\;k \over k-1}$ (如果 ${\displaystyle k\leq 1}$, 期望值为无穷大) 且随机变量的标准差为 ${\displaystyle {x_{\min } \over k-1}{\sqrt {k \over k-2}}}$ (如果 ${\displaystyle k\leq 2}$, 标准差不存在)。

被认为大致是帕累托分布的例子有：

• 财富在个人之间的分布
• 人类居住区的大小
• 对维基百科条目的访问
• 接近绝对零度时，玻色–爱因斯坦凝聚的团簇
• 在互联网流量中文件尺寸的分布
• 油田的石油储备数量
• 龙卷风带来的灾难的数量