库拉托夫斯基定理

库拉托夫斯基定理（英語：）是一个关于平面图的等价判定定理，它由波兰数学家卡齐米日·库拉托夫斯基提出[1]。这个定理表明，一个图是平面图当且仅当它不包含K5 或 K3,3的细分。其中，K5是包含5个顶点的完全图，K3,3是包含6个顶点的完全二分图，其中三个顶点和另外三个顶点两两相连，K3,3也被称作utility graph。

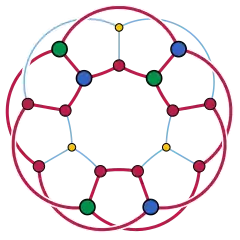
广义佩特森图 G(9,2)中包含K3,3的细分, 说明广义佩特森图不是平面图.

进一步阐述

平面图（planar graph)是可以画在平面上，使得不同的边在除了端点之外互不相交的图。

细分(subdivision)是在一个图的一些边上加入一些点，使得这些边被分割成包含一条或多条边的路径。库拉托夫斯基定理表明，一个图G是平面图，如果它不能通过细分K5或 K3,3的边，然后再加上一些多余的边或点得到。等价地，一个图是平面图当且仅当它不包含同胚（Homeomorphism）于K5 或 K3,3的子图。

库拉托夫斯基子图

G是一个图，如果它包含K5或 K3,3的细分H，那么H被称为G的一个库拉托夫斯基子图。[2]

K5和 K3,3均不是平面图，这可以分类讨论或利用欧拉公式进行验证。此外，细分一个非平面图不可能得到一个平面图。这是显然的，如果一个图G的细分G′有平面画法，那么把G′中通过细分边e得到的路径的平面曲线段当作原图G边e的平面曲线段，我们也可以得到G的一个平面画法。因此，一个包含库拉托夫斯基子图的图不是平面图。定理的另一边证明则更加困难。

相关结论

库拉托夫斯基定理和另一个平面图等价判定定理瓦格纳定理(Wagner's theorem)[3]高度相关。瓦格纳定理表明，一个图是平面图当且仅当 K5 或 K3,3 不是它的次图（minor）。次图又称图子式，如果无向图H可以通过图G删除边和顶点或收缩边得到，则称H为G的子式或次图。

显然，如果图G包含库拉托夫斯基子图，那么K5 或 K3,3一定是它的子式。反之，可以验证任意包含K5 或 K3,3子式的图G也必然包含库拉托夫斯基子图[4]。因此，两个定理实际上是等价的。

參考資料
  1. Kuratowski, Kazimierz, (PDF), Fund. Math., 1930, 15: 271–283 [2020-12-22], （原始内容存档 (PDF)于2018-07-23） （法语）.
  2. Tutte, W. T., , Proceedings of the London Mathematical Society, Third Series, 1963, 13: 743–767, MR 0158387, doi:10.1112/plms/s3-13.1.743.
  3. Wagner, K., , Math. Ann., 1937, 114: 570–590, doi:10.1007/BF01594196
  4. Bondy, J. A.; Murty, U.S.R., , Graduate Texts in Mathematics 244, Springer: 269, 2008, ISBN 9781846289699.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.