康威準則

康威準則是英國數學家約翰·何頓·康威提出的密鋪數學理論，描述多邊形可用來做平面镶嵌的條件，包括以下幾點[1]。多邊形需要是閉合多邊形，在邊界上有六個點A, B, C, D, E及F，且滿足以下條件：

  • 邊界AB的和邊界ED全等。
  • 邊界BC, CD, EF及FA都是中心对称图形，若對其中心點旋轉180度，和原來圖形重合。
  • 六個點中至少要有三個點是相異的，另外三點可以共點[2]。
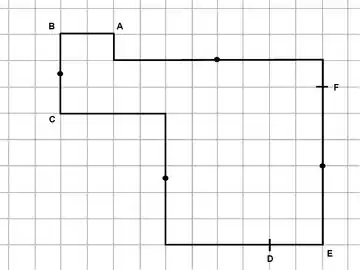
一個符合康威準則的直角多邊形，其中四個中心对称图形的中心點以黑點表示

任何滿足康威準則的多邊形，都可以只用此多邊形規律密鋪（periodic tiling），多邊形只需平移以及做180度的旋轉。康威準則是多邊形可用來做平面镶嵌的充份條件，但不是必要條件，存在一些多邊形可以做平面镶嵌，但不符合康威準則的情形[3]。

範例
這兩種九格骨牌不符合康威準則，但仍可以做平面密鋪
用中心对称六邊形進行的六邊形鑲嵌
另一種六邊形鑲嵌，此處的六邊形不是中心对称六邊形

以康威準則來看，最直覺的符合康威準則的是有一對全等平行對邊的六邊形，稱為六邊形鑲嵌[4]。不過若有些點重合，這個準則也可以用在其他的多邊形（如三角形、四邊形），甚至是其外形有曲線的形狀[5]。

康威準則可以找出多種可做多邊形規律密鋪的多邊形，甚至包括非凸多邊形。但右邊的二種九格骨牌不符合康威準則，仍可以進行規律密鋪。因此康威準則只是多邊形規律密鋪的充份條件，但不是必要條件。

多格骨牌中，二格骨牌到九格骨牌中都至少有一個符合康威準則，可以規律密鋪的骨牌[3]。

相關條目
  • 平行多邊形：可以在只靠平移（不考慮旋轉180度）的情形下，用平行多邊形密鋪整個平面。

参考文献
  1. Will It Tile? Try the Conway Criterion! by Doris Schattschneider Mathematics Magazine Vol. 53, No. 4 (Sep., 1980), pp. 224-233
  2. . [2015-07-19]. （原始内容存档于2014-05-20）.
  3. . [2015-07-19]. （原始内容存档于2015-09-24）.
  4. Polyominoes: A Guide to Puzzles and Problems in Tiling, by George Martin, Mathematical Association of America, Washington, DC, 1991, p. 152, ISBN 0883855011
  5. The five types of Conway Criterion polygon tile （页面存档备份，存于）, PDF file

外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.