康威立方

康威立方（）是一個立體的包裝問題，得名自其發明者，數學家約翰·何頓·康威。康威立方要將13個1 × 2 × 4的方塊、1個2 × 2 × 2的方塊、1個1 × 2 × 2的方塊及3個1 × 1 × 3的方塊放在一個5 × 5 × 5的立方體空間中[1]。

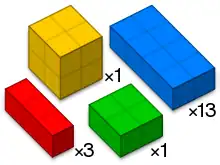
康威立方中用到的四種立方體。

解法
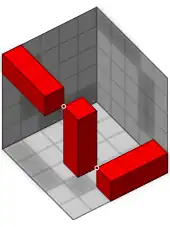
一種有關三塊1×1×3方塊的可能排列方式

基於奇偶數的考量，每個5×5×1的區域中都要出現1×1×3方塊的一部份，而所占空間需為奇數，只要注意到上述的特點，即可求解康威立方[2]。此特性和斯洛陶伯－赫拉茨马立方有些類似。

相關條目

外部連結

參考資料
  1. . Wolfram MathWorld. [2007-03-14]. （原始内容存档于2022-06-19）.
  2. Elwyn R. Berlekamp, John H. Conway and Richard K. Guy: winning ways for your mathematical plays, 2nd ed, vol. 4, 2004.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.