开世定理

${\displaystyle t_{12}\cdot t_{34}+t_{14}\cdot t_{23}-t_{13}\cdot t_{24}=0}$

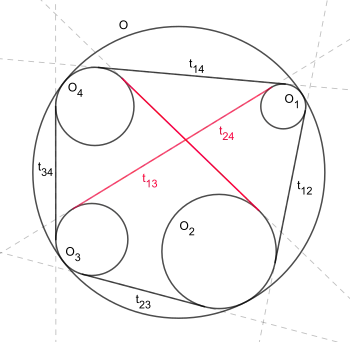
开世定理的背景是圆的内切圆。设有半径为${\displaystyle \,R}$ 的一个圆${\displaystyle \,O}$，圆内又有四个圆${\displaystyle \,O_{1},O_{2},O_{3},O_{4}}$ 内切于圆${\displaystyle \,O}$（如右图）。如果将圆${\displaystyle \,O_{i},O_{j}}$ 的外公切线的长度设为${\displaystyle \,t_{ij}}$，那么开世定理声称，有下列等式成立。

${\displaystyle \,t_{12}\cdot t_{34}+t_{14}\cdot t_{23}=t_{13}\cdot t_{24}}$

可以注意到，如果四个内切的圆都退化成点的话，就会变成圆${\displaystyle \,O}$ 上的四个点，而开世定理中的等式也会化为托勒密定理。

设大圆的圆心是点${\displaystyle \,O}$；四个圆的圆心分别是点${\displaystyle \,O_{1},O_{2},O_{3},O_{4}}$，半径分别是${\displaystyle \,R_{1},R_{2},R_{3},R_{4}}$。每个圆与大圆${\displaystyle \,O}$ 的切点分别是${\displaystyle \,K_{1},K_{2},K_{3},K_{4}}$。

首先，根据勾股定理可以推出：对于任意的i 和j，都有

${\displaystyle \,t_{ij}^{2}={\overline {O_{i}O_{j}}}^{2}-(R_{i}-R_{j})^{2}\qquad \qquad \qquad \cdots \,\,(1)}$

接下来的思路是将这个公式右边的各个长度用${\displaystyle \,K_{i},K_{j}}$ 来表示。

考虑三角形${\displaystyle \,O_{i}OO_{j}}$，根据三角形的余弦定理：

${\displaystyle {\overline {O_{i}O_{j}}}^{2}={\overline {OO_{i}}}^{2}+{\overline {OO_{j}}}^{2}-2{\overline {OO_{i}}}\cdot {\overline {OO_{j}}}\cdot \cos \angle O_{i}OO_{j}\qquad \qquad \qquad \cdots \,\,(2)}$

由于每个圆${\displaystyle \,O_{i}}$ 都和大圆相切，所以：

${\displaystyle {\overline {OO_{i}}}=R-R_{i},\,\angle O_{i}OO_{j}=\angle K_{i}OK_{j}}$

设点${\displaystyle \,C}$ 为大圆${\displaystyle \,O}$ 上的任意一点，根据三角形的正弦定理，在三角形${\displaystyle \,K_{i}CK_{j}}$之中，有：

${\displaystyle {\overline {K_{i}K_{j}}}=2R\cdot \sin \angle K_{i}CK_{j}=2R\cdot \sin {\frac {\angle K_{i}OK_{j}}{2}}}$

所以，余弦式

${\displaystyle \cos \angle K_{i}OK_{j}=1-2\sin ^{2}{\frac {\angle K_{i}OK_{j}}{2}}=1-2\cdot \left({\frac {\overline {K_{i}K_{j}}}{2R}}\right)^{2}=1-{\frac {{\overline {K_{i}K_{j}}}^{2}}{2R^{2}}}}$

将以上${\displaystyle {\overline {OO_{i}}}}$ 与${\displaystyle \cos \angle K_{i}OK_{j}}$ 代入式子${\displaystyle (2)}$中，就可以得到：

${\displaystyle {\overline {O_{i}O_{j}}}^{2}=(R-R_{i})^{2}+(R-R_{j})^{2}-2(R-R_{i})(R-R_{j})\left(1-{\frac {{\overline {K_{i}K_{j}}}^{2}}{2R^{2}}}\right)}$

${\displaystyle =(R-R_{i})^{2}+(R-R_{j})^{2}-2(R-R_{i})(R-R_{j})+(R-R_{i})(R-R_{j})\cdot {\frac {{\overline {K_{i}K_{j}}}^{2}}{R^{2}}}}$

${\displaystyle =((R-R_{i})-(R-R_{j}))^{2}+(R-R_{i})(R-R_{j})\cdot {\frac {{\overline {K_{i}K_{j}}}^{2}}{R^{2}}}}$

${\displaystyle =(R_{i}-R_{j})^{2}+(R-R_{i})(R-R_{j})\cdot {\frac {{\overline {K_{i}K_{j}}}^{2}}{R^{2}}}}$

再代入式子${\displaystyle (1)}$中，就得到${\displaystyle t_{ij}}$的表达式：

${\displaystyle t_{ij}={\sqrt {{\overline {O_{i}O_{j}}}^{2}-(R_{i}-R_{j})^{2}}}={\frac {{\sqrt {R-R_{i}}}\cdot {\sqrt {R-R_{j}}}\cdot {\overline {K_{i}K_{j}}}}{R}}}$

以上等式对所有的i 和j 都成立，因此只要注意到四边形 ${\displaystyle \,K_{1}K_{2}K_{3}K_{4}}$ 是圆内接四边形，那么对其应用应用托勒密定理就可以得到开世定理：

${\displaystyle t_{12}t_{34}+t_{14}t_{23}={\frac {1}{R^{2}}}\cdot {\sqrt {R-R_{1}}}{\sqrt {R-R_{2}}}{\sqrt {R-R_{3}}}{\sqrt {R-R_{4}}}\left({\overline {K_{1}K_{2}}}\cdot {\overline {K_{3}K_{4}}}+{\overline {K_{1}K_{4}}}\cdot {\overline {K_{2}K_{3}}}\right)}$

${\displaystyle ={\frac {1}{R^{2}}}\cdot {\sqrt {R-R_{1}}}{\sqrt {R-R_{2}}}{\sqrt {R-R_{3}}}{\sqrt {R-R_{4}}}\left({\overline {K_{1}K_{3}}}\cdot {\overline {K_{2}K_{4}}}\right)=t_{13}t_{24}}$

证明完毕。

可以用类似的方法证明，只要当圆${\displaystyle \,O_{1},O_{2},O_{3},O_{4}}$ 与大圆${\displaystyle \,O}$ 相切（不论是外切还是内切），就会有类似开世定理的等式成立。这是需要注明，对任意的i 和j：

如果圆${\displaystyle \,O_{i},O_{j}}$ 是与大圆${\displaystyle \,O}$ 以同样的方式相切（都是外切或者都是内切）的话，则${\displaystyle \,t_{ij}}$表示两个圆的外公切线的长度；

如果圆${\displaystyle \,O_{i},O_{j}}$ 是与大圆${\displaystyle \,O}$ 以不同的方式相切（一个是外切而另一个是内切）的话，则${\displaystyle \,t_{ij}}$表示两个圆的内公切线的长度。

另一个特点是：这定理的逆定理也成立。也就是说，如果开世定理的等式成立，那么这些圆必定以规定的方式与大圆相切。[1]

在欧几里得几何学中，开世定理可以用来证明多种不同的结论。比如说费尔巴哈定理的一个简洁证明中就用到了它。

• （英文） Roger A. Johnson. . Dover. 2007. ISBN 978-0-486-46237-0.，p.123-125 （1929年曾以《现代几何学》（modern geometry）之名出版。）.
• （英文）O. Bottema, Reinie Erne. . Springer. 2008. ISBN 978-0-387-78130-3.

• 埃里克·韦斯坦因. . MathWorld.
• Shailesh Shirali: On a generalized Ptolemy Theorem