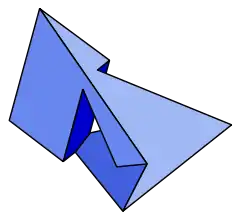
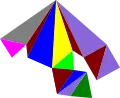
恰薩爾十四面體
恰薩爾十四面體是一種可以對應到拓撲环面的非凸多面體,由阿科斯·恰薩爾於1949年發現。[1]這個多面體中間有一個孔洞,由14個不等邊三角形面組成。特別地,這個多面體不存在對角線,也就是說任兩個頂點之間所形成的線段都位於其表面邊界上,同時,其也對應到七的頂點的完全圖。[2]:139-143
 | ||||
| 類別 | 环形多面体 | |||
|---|---|---|---|---|
| 對偶多面體 | 希洛西七面體 | |||
| 性質 | ||||
| 面 | 14 | |||
| 邊 | 21 | |||
| 頂點 | 7 | |||
| 歐拉特徵數 | F=14, E=21, V=7 (χ=0) | |||
| 虧格 | 1 | |||
| 組成與佈局 | ||||
| 面的種類 | 2個等邊三角形 2個等腰三角形 10個鈍角三角形 | |||
| 面的佈局 | 3.3.3.3.3.3 | |||
| 對稱性 | ||||
| 對稱群 | C1, [ ]+, (11) | |||
| 特性 | ||||
| 非凸 | ||||
| 圖像 | ||||
| ||||
性質

恰薩爾十四面體的正交投影圖。 在其SVG圖像中可用滑鼠轉動以便觀察整個模型
恰薩爾十四面體由14個面、21條邊和7個頂點組成。在這七個頂點中,每個頂點都是6個三角形的公共頂點,其可以分成3組和一個單獨的頂點,三組兩兩相等,與其對偶多面體——希洛西七面體的面對應[3]。在其14個面中,有2個等邊三角形、2個等腰三角形和10個鈍角三角形。[3]
完全圖
恰薩爾十四面體是一種不存在對角線的流形多面體結構。[1]也就是說,對恰薩爾十四面體的所有頂點而言,任意兩個頂點間皆有一條邊連接,因此這個多面體不存在任何不在邊界上且連接兩個頂點的線段。這種性質目前已知僅有正四面體和恰薩爾十四面體擁有。這種性質在圖論中稱為完全圖,也就是說恰薩爾十四面體可以對應到七個頂點的完全圖。[4][5]
若一個在一個有h個孔洞的環面構建一個邊界包含v個頂點的多面體,且所有頂點中任兩個頂點間都有邊相連,則其部分的歐拉特徵數會具有以下關係:[6]
對於零個孔、四個頂點(h=0、v=4)的四面體和1個孔、7個頂點(h=1、v=7)的恰薩爾十四面體都滿足這個方程。下一個可能的整數解是6個孔、12個頂點(h=6、v=12)具有44個面和66個條邊的多面體。然而目前並不知道是否存在實體的多面體滿足這個特性,而非僅能以抽象多面體的方式存在。更無法確定這樣的多面體是否能在更高虧格的環面下存在。[7]更一般地,當v除以12餘0、3、4或7時,上述等式給出的h值皆為整數。[8]
參見
參考文獻
- Császár, A., (PDF), Acta Sci. Math. Szeged, 1949, 13: 140–142 [2021-09-08], 原始内容存档于2017-09-18.
- Gardner, Martin, , W. H. Freeman and Company, 1988, ISBN 0-7167-1924-X
- . dmccooey.com. [2021-07-30]. (原始内容存档于2021-09-08).
- Alexander Bogomolny. . Interactive Mathematics Miscellany and Puzzles. [2021-09-08]. (原始内容存档于2021-08-14).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Martin Gardner. . Scientific American (Scientific American, a division of Nature America, Inc.). 1975, 232 (5): 102–108 [2021-09-08]. ISSN 0036-8733. (原始内容存档于2021-09-08).ISSN 1946-7087.
- Ziegler, Günter M., , Bobenko, A. I.; Schröder, P.; Sullivan, J. M.; Ziegler, G. M. (编), , Oberwolfach Seminars 38, Springer-Verlag: 191–213, 2008, ISBN 978-3-7643-8620-7, arXiv:math.MG/0412093
 , doi:10.1007/978-3-7643-8621-4_10
, doi:10.1007/978-3-7643-8621-4_10 - Lutz, Frank H., , Electronic Geometry Models, 2001: 2001.02.069 [2021-09-08], (原始内容存档于2022-01-19)
- L. Szilassi. (PDF). Symmetry: Culture and Science (Department of Mathematics, Faculty of Mechanical Engineering, Slovak University of Technology in Bratislava). 2000, 11 (1–4): 317–335 [2021-09-08]. (原始内容存档 (PDF)于2016-06-09).
- . dmccooey.com. [2021-09-08]. (原始内容存档于2021-09-08).
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Gardner, Martin. . Scientific American (SCI AMERICAN INC 415 MADISON AVE, NEW YORK, NY 10017). 1975, 232 (5): 102–107.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.