伯努利定律
伯努利原理(英語:),又稱白努利定律或柏努利定律(英語:)[1],是流體力學中的一個定律,由瑞士流體物理學家丹尼尔·伯努利於1738年出版他的理論《Hydrodynamica》,描述流體沿著一條穩定、非黏性、不可壓縮的流線移動行為。[2]
在流體動力學,伯努利原理指出,無黏性的流體的速度增加時,流體的壓力能或位能(勢能)總和將減少。
伯努利原理可以應用到不同類型的流體流動,從而是可廣泛套用的伯努利方程表示式。事實上,有不同類型的伯努利方程式不同形式的。伯努利原理的簡單形式是有效的不可壓縮流動(如液體流動),也為移動可壓縮流體(如氣體)在低馬赫數(通常小於0.3)。更先進的形式可被應用到在某些情況 下,在更高的馬赫數(見伯努利方程的推導)可壓縮流。
伯努利定律可以從能量守恆定律來推演。說明如下:在一個穩定的水流,沿著直線流向的所有點上,各種形式的流體機械能總和必定相同。也就是說,動能,位能,與內能的總和保持不變。換言之,任何的流體速度增加,即代表動態壓力和單位體積動能的增加,而在同時會導致其靜態壓力,單位體積流體的位能、內能等三者總和的減少。如果液體流出水庫,在各方向的流線上,各種形式的能量的總和是相同的;因為每單位體積能量的總和(即壓力和單位體積流體的重力位能的總和)在水庫內的任何位置都相同。
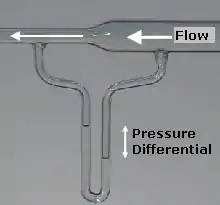
伯努利原理,也可以直接由牛頓第二定律推演。說明如下:如果從高壓區域往低壓區域,有一小體積流體沿水平方向流動,小體積區域後方的壓力自然比前方區域的壓力更大。所以,此區域的力量總和必然是沿著流線方向向前。在此假設,前後方區域面積相等,如此便提供了一個正方向淨力施於原先設定的流體小體積區域,其加速度與力量同方向。此假想環境中,流體粒子僅受到壓力和自己質量的重力之影響。先假設如果流體沿著流線方向作水平流動,並與流體流線的截面積垂直,因為流體從高壓區域朝低壓區域移動,流體速度因此增加;如果該小體積區域的流速降低,其唯一的可能性必定是因為它從低壓區朝高壓區移動。因此,任一水平流動流體之內,壓力最低處有最高流速,壓力最高處有最低流速。
物理量及定律
推論過程
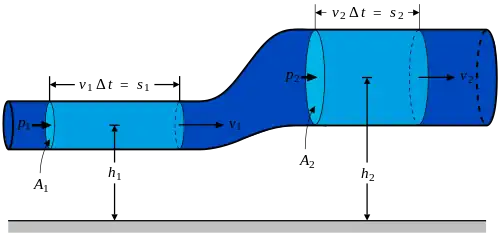
考慮一符合上述假設的流體,如圖所示:
流體因受壓力的推動而得之能量:
流體因重力做功所損失的能量:
流體所得的動能可以改寫為:
根據能量守恆定律,流體因受力所得的能量+流體因重力做功所損失的能量=流體所得的動能。
由連續方程式可知:
令
從等式兩邊除以 及可得:
或
垂直流線方向的加速度定律
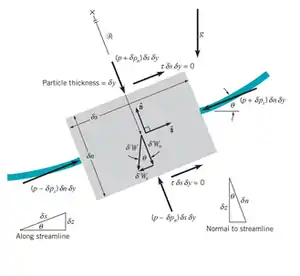
考慮沿流線運動的微小流體質點[3],其質量以表示,δy代表寬度,流體質點運動以速度向量V表示,流線座標可表示為與某參考點的距離s=s(t)及流線局部曲率半徑 ,沿著流線的座標為s;垂直流線的座標為 n。
在垂直流線的方向n̂上,由於存在向心加速度,故質點所受淨力為:
,其中為微小流體質點體積,為流體密度。
而質點所受重力為:
,其中。
如圖所示的質點中央壓力為p ,垂直流線的兩端平均壓力分別為及,可用泰勒級數展開求壓力差異。
為質點於垂直方向上所受淨壓
故
因為沿著垂直流線方向 ,可得到垂直流線方向之運動方程式
此式意味著,垂直於流線的壓力梯度及質點所受重力會改變流向,造成彎曲的流線。
若忽略重力的因素,即只考慮流體在水平面的流動,以龍捲風為例,,會得到,這意味著,壓力隨著遠離曲率中心的距離而增大(n的正向,指向彎曲流線的內部),由於為正值,因此會是負的,在龍捲風之外的壓力(典型的大氣壓力)遠大於中心處(低氣壓,可能會產生部分真空),而這些壓力差會被用於平衡曲率運動所需的向心力。
在s為定值的情況下
沿n的方向積分可得
對於不可壓縮流,可得
由推導方程式所需的基本假設:穩定、無黏性 及不可壓縮流,可以得出
1.跨過流線的運動方程式
2.沿著流線的運動方程式 同上述做法[3],可得出沿著流線方向之運動方程式
以及伯努利定律
在跨過流線的情形使用伯努力定律時,若流體位置發生旋轉或彎曲,就會因跨過流線的運動方程式中所含的,導致計算結果須修正。
特例:托里切利定律
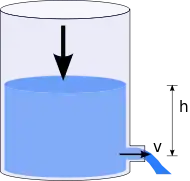
當液體因受到地心吸力的作用而流出時,其速度等於,其中為重力加速度,為開口的中心和液體最高面的距離。[4]這個速度剛好等於液體從離地的地方以自由落體的方式下落時著地前的速度(但實際上因為有空氣阻力,所以實際情形一般不會以自由落體的方式下落)。
伯努利定律演示實驗


簡易噴霧器,以大吸管固定兩隻小吸管使之夾角略小於直角,因從吸管吹出之氣體流速較快,壓力較一大氣壓力為低,因此能夠將水經由下端吸管中吸起,並於開口處加速破碎成霧滴,模型製作用噴槍以及工業用噴漆噴槍多為此種設計。
不過因為伯努利定律是假設流體沿著流線流動,探討同一流線上二點的速度及壓力變化。因此有些現象和伯努利定律無關,例如懸浮保麗龍球,將可折彎的吸管一端向上穩定吹出氣體,將一直徑約3公分之保麗龍球放置於氣柱上,保麗龍球能夠懸浮晃動於一定區域中,因為保麗龍球上方和下方的氣流不是同一流線,這和伯努利定律無關,是康達效應的結果[5]。
可壓縮流體的伯努利定律
伯努利從觀察液體的行為中推導出伯努利方程式,但他的方程是只能應用在不可壓縮的流體,以及雖然可壓縮但流速非常慢的流體(也許可以到1/3的聲速)。利用基本物理原理,可以發展出類似的方程式,以適用於可壓縮的流體。以下有幾個類似於伯努力定律,能應用在不同領域方程式。它們的推導只運用了像是牛頓第二定律和熱力學第一定律的基本物理定律。
可壓縮流體之流體力學
對於可壓縮的流體,在保守力的作用之下,所得到的守恆式為
- (流線型下的守恆)
其中:
在工程領域,在海拔比較高的地方,其壓力會比地表來的小,而且流體流動的時間通常是相當的小,如同絕熱系統般。在這種情形下,上述的方程即
- (流線型下的守恆)
其中:
在可壓縮流體可以應用的地方,因為高度變化與其他變因相比小的很多,故gz項可以省略,所以較常用的方程式為
其中:
- 總壓力
- 總密度
參考資料
- . [2017-11-22]. (原始内容存档于2017-06-27).
- 白努利定理的誤解與錯誤 物理雙月刊
- BRUCE R. MUNSO; DONALD F. YOUNG;THEODORE H. OKIISHI;WADE W. HUEBSCH. . John Wiley & Sons Inc. 2013-01-22: page 96. ISBN 1118318676.
- Dennis Zill. . Jones & Bartlett. 2012: 第22頁. ISBN 9781449689803.
- 張慧貞 物理雙月刊 37卷3期 教科書對於演示實例的理解及誤解
延伸閱讀
- Ting, J. . createspace. 2014 [2016-11-14]. ISBN 978-149426094-1. (原始内容存档于2021-05-05).
- Batchelor, G.K. . Cambridge University Press. 1967. ISBN 0-521-66396-2.
- Clancy, L.J. . Pitman Publishing, London. 1975. ISBN 0-273-01120-0.
- Lamb, H. 6th. Cambridge University Press. 1993. ISBN 978-0-521-45868-9. Originally published in 1879; the 6th extended edition appeared first in 1932.
- Landau, L.D.; Lifshitz, E.M. . Course of Theoretical Physics 2nd. Pergamon Press. 1987. ISBN 0-7506-2767-0.
- Chanson, H. . CRC Press, Taylor & Francis Group. 2009 [2015-01-06]. ISBN 978-0-415-49271-3. (原始内容存档于2011-08-07).
外部連結
| 维基共享资源上的相关多媒体资源:伯努利定律 |
- Head and Energy of Fluid Flow (页面存档备份,存于)
- Bernoulli equation calculator
- Denver University – Bernoulli's equation and pressure measurement (页面存档备份,存于)
- Millersville University – Applications of Euler's equation
- NASA – Beginner's guide to aerodynamics (页面存档备份,存于)
- Misinterpretations of Bernoulli's equation – Weltner and Ingelman-Sundberg (页面存档备份,存于)