振鈴效應

在信號處理中，特別是數位影像處理 ，振鈴效應是一種出現在信號快速轉換時，附加在轉換邊緣上導致失真的信號。而在圖像或影像上，振鈴效應會導致出現在邊緣附近的環帶或像是「鬼影」的環狀偽影，称为振铃伪像[1]（ringing artifact）；在音訊中，振鈴效應會導致出現在短暫音附近的回聲，特别是由打擊樂器發出的聲音；最容易注意到的是預回聲。使用「振鈴」這一個詞則是因為輸出信號在輸入信號快速轉換的邊緣附近出現一有一定衰減速度的振盪，這個現象相似於鐘被敲擊之後發出聲音的過程。振鈴效應就如同其他的失真一樣，他們的最小化在濾波器設計中是很重要的一項指標。

圖片顯示為振鈴效應產生的環狀偽影。在顏色變換的兩邊各有3個等級：過衝，第一環，和(較微弱的)第二環。
沒有振鈴效應的相同圖片。

介紹
造成振鈴效應的主要原因是濾波器階躍響應中的過衝及振盪。

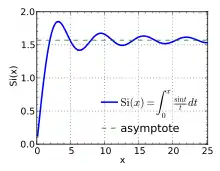
造成振鈴效應的主要原因是信號的頻寬限制（具體而言，不具有高頻信號成分）或是信號通過一個低通濾波器；這是在頻域上的解釋。而在時域上的討論，產生振鈴效應的原因則是因為Sinc函數中的漣波，[2] 即為一個完美低通濾波器的脈衝響應（在時域中的形式）。在數學上這叫做吉布斯現象。

當信號轉換速度加劇的時候，我們可以在振鈴中區別出過衝（和下衝），過衝時輸出信號較輸入訊號高，而在過衝之後，信號因為過度修正而變得低於目標數值，之後來回振盪；這些現象往往會同時發生，因此常常被混用，而被共同稱為「振鈴」。

振鈴這一個詞最常被使用在時域上的漣波，但有時也被用在討論頻域上的影響：[3] 在時域中使用矩形函數的濾波器會導致在頻域中的漣波，其原因就如同Sinc濾波器（在頻域中為矩形函數）在時域中產生的漣波一樣；在這兩個例子中，矩形函數的傅立葉變換就是Sinc函數。

原因

描述
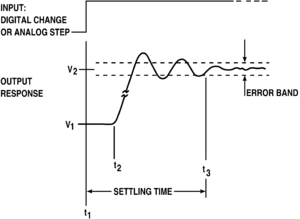
圖為Sinc函數，是理想低通濾波器的脈衝響應，可以看到在脈衝兩旁有漣波。
圖為吉布斯現象，顯示階躍函數中的漣波。

依照定義，振鈴發生在一個非振盪的輸入信號產生振盪輸出時：嚴謹來說，當一個輸入信號在一定時間之內是單調時，其輸出信號非單調。這個現象在一濾波器的脈衝響應或是階躍響應有振盪時最嚴重；簡單來說，若輸入一個尖峰信號，相當於一個快速的輸入變化，則輸出會有明顯的振盪。

振鈴效應和過衝及下衝很有關係，即輸出的值超過輸入數值的最大值（相對地，即低於輸入數值的最小值）：兩者可以單獨出現，但在許多重要的狀況中，像是低通濾波器，會首先有一個過衝，然後響應會跳到穩態之下而產生第一個漣波，然後再穩態附近來回振盪。因此過衝是這個現象的第一步，而第二步之後才是振鈴效應。由於兩個現象有密切的關連，所以這兩個詞常常被混用：振鈴同時包含第一個過衝和後面連續出現的漣波。

如果了解線性非時變（LTI）濾波器，則可以從兩個方面來了解濾波器其振鈴效應：脈衝響應（時域的觀點），或頻率響應（頻域的觀點，即脈衝響應的傅立葉變換）。振鈴效應是一種時域中的現象，而在濾波器設計中，他和一些重要的頻域特性有權衡關係（trade-off）；當使用所要的頻率響應時會產生振鈴效應，然而當要抑制振鈴效應時則無法地到所要的頻率響應。

Sinc濾波器
從正弦積分可以看出振盪。

解釋振鈴效應最好的例子是理想低通濾波器，也就是Sinc濾波器。理想低通濾波器的脈衝響應和階躍響應（脈衝響應的積分）中可以看到很明顯的振盪，因此他的積分（即正弦積分）也有很明顯的振盪特徵。

這些振鈴效應的產生並不是因為實作上或窗函數應用上的不理想：理想的低通濾波器在處理所想要的頻率響應時，必然會在時域中產生振鈴效應。

優點
人為地在左邊的方塊周圍加入過衝可以增加銳度。

雖然振鈴效應一般來說被认為是一種不理想的現象，但在轉換時的第一個過衝可以透過增加轉換時的斜率來增加銳度（視銳度），而因此被視為一種優點。[4]

例子

JPEG
圖為一個JPEG失真的極端例子，其中包括振鈴效應：青色(即為白色減去紅色)環繞在紅色星星的周圍。
離散餘弦變換的基底函數。

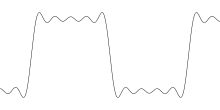
JPEG壓縮會在急遽地轉換中產生振鈴效應，這個現象在文字圖像中尤其容易發現。

這是因為信號失去了高頻成分而產生的，就如同在階躍函數中產生的振鈴現象一樣。JPEG使用8×8的區塊，並對其中的每一個區塊使用離散餘弦變換（DCT）。DCT是一種和傅立葉變換相關的變換，而振鈴效應的發生是因為損失了高頻的信號成分或是高頻成分的精確度有所損失。

振鈴現象也可能發生在圖像的邊緣：由於JPEG圖像分成8×8區塊，如果圖像不能被分成整數個區塊，則圖像的編原則沒有辦法輕易地進行編碼，而一些解決方法，例如在輸入圖片的邊緣填充一些黑色，但這樣會在邊緣產生急遽的轉變，進而在編碼後的圖片中產生振鈴效應。

振鈴效應也會發生在使用小波分析的JPEG2000中。

一些相關的圖像：

圖像 非破壞性壓縮 破壞性壓縮
原始圖像
利用Canny邊緣探測

處理後凸顯的失真。

預回聲
預回聲發生在打擊樂器聲中，例如鈸。

在音頻信號處理，振鈴效應可能導致發生在聲音瞬變前或後的回聲，例如從打擊樂器發出的短促的聲音，如鈸（這是脈衝振鈴）。發生在瞬變後的回聲（遵守因果的）是聽不到的，因為他被瞬變遮蔽了，這種效應被稱為時域掩蔽。 因此只有發生在瞬變後的回聲（違反因果的）會被聽到，而這種現象被稱為預回聲。

這種現象發生在使用傅立葉變換相關變換的音訊壓縮算法中，如MP3，AAC和 Vorbis，被視為一種壓縮失真。

相似的現象

也會有其他現象有著類似振鈴效應的特徵，但這些現象在成因卻有很大的不同。在某些情況下，我們可以在一個點的周圍看到環狀偽影，這些可能會被認為是「環」（正式來說是環形），然而這個和在本頁討論的「振鈴」（振盪衰減）這種頻率現象並沒有關係。（環、振鈴在英文中皆使用ring一詞。）

邊緣銳化

邊緣銳化的目的是要加強邊緣的對比度，而這可能會造成類似振鈴現象。這是由高通濾波器產生的，而非低通濾波器。[5]

特殊函數
由夫朗和斐繞射造成的艾里斑。

有許多特殊函數都有振盪衰減的特徵，因此當與這一類函數做摺積時會產生有類似振鈴效應的輸出；有些人會認為這是振鈴效應，或是歸類的頻域信號處理的非預期的不理想效應。

夫朗和斐繞射產生的艾里斑的分布是點擴散函數，而該函數中可以看到振盪。

圖中顯示幾個第一類貝索函數，可以看到函數中有振盪。

在和艾里函數相關的第一類貝索函數中可以看到振盪衰減。

離焦和球面像差的組合可以看到類似振鈴的現象。

在相機攝影中、組合離焦（defocus）和球面像差可以產生環狀的圖案。然而，這些圖案不一定和（本頁討論的）振鈴效應相似，這些圖案可以是振盪衰減（圓環狀的衰減能量強度），或是其他的能量強度分布，例如單一的明亮帶。

干擾

鬼影是電視干擾的其中一種，會在畫面中看到重覆（重疊）的影像。雖然這不是一種振鈴效應，但是它可以被表示為與函數的摺積。該函數在原點的值為1，而在一定距離有值ε（與鬼影的能量強度有關），這個函數和前面某些函數有一定程度的相似（一個單一的峰值，而不是連續的振盪）。

鏡頭光暈
鏡頭光暈

在攝影中，鏡頭光暈是一種缺陷，其特徵是在強光源附近出現許多圓圈，並在照片中有因不需要的光源（例如透鏡中元件的反射和散射）產生的鬼影。

視覺假象
馬赫帶效應

視覺假象可能發生在轉變，像是馬赫帶效應。馬赫帶效應可以在感覺上呈現出類似於吉布斯現象中的過衝/下衝。

參考資料
  1. . [2023-07-16]. （原始内容存档于2023-07-16）.
  2. Bankman, Isaac N., , Academic Press, 2000, ISBN 978-0-12-077790-7, section I.6, Enhancement: Frequency Domain Techniques, p. 16 （页面存档备份，存于）
  3. Digital Signal Processing （页面存档备份，存于）, by J.S.Chitode, Technical Publications, 2008, ISBN 978-818-431-346-8, 4 - 70 （页面存档备份，存于）
  4. Mitchell, Don P.; Netravali, Arun N. (PDF). ACM SIGGRAPH International Conference on Computer Graphics and Interactive Techniques 22 (4): 221–228. August 1988 [2016-06-22]. ISBN 0-89791-275-6. doi:10.1145/54852.378514. （原始内容存档 (PDF)于2021-02-24）.
  5. Microscope Image Processing （页面存档备份，存于）, by Qiang Wu, Fatima Merchant, Kenneth Castleman, ISBN 978-012-372-578-3 p. 71 （页面存档备份，存于）
  • Allen, Ronald L.; Mills, Duncan W., , Wiley-IEEE, 2004, ISBN 978-0-471-23441-8
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.