接触力学

球体和弹性半空间的接触

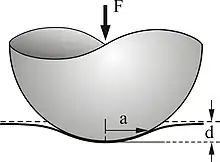
一个半径为 ${\displaystyle R}$ 的球体在一个弹性半空间上压出的凹痕深度为 ${\displaystyle d}$ ，若产生的接触区域的半径为 ${\displaystyle a={\sqrt {Rd}}}$ ，则作用力 ${\displaystyle F}$ 为 ${\displaystyle F={\frac {4}{3}}E^{*}R^{1/2}d^{3/2}}$ ,

式中

${\displaystyle {\frac {1}{E^{*}}}={\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}}$ .

${\displaystyle E_{1}}$,${\displaystyle E_{2}}$ 分别为是接触体的弹性模量，${\displaystyle \nu _{1}}$,${\displaystyle \nu _{2}}$ 是泊松比。

两个球体的接触

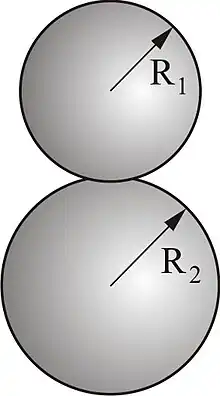
若给定两个球体的半径为 ${\displaystyle R_{1}}$ 和 ${\displaystyle R_{2}}$, 定义 ${\displaystyle R}$ 为

${\displaystyle {\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}$ ,

则接触区域的压力分布为

${\displaystyle p=p_{0}\left(1-{\frac {r^{2}}{a^{2}}}\right)^{1/2}}$ , 式中

${\displaystyle p_{0}={\frac {2}{\pi }}E^{*}\left({\frac {d}{R}}\right)^{1/2}}$ .

对于 ${\displaystyle \nu =0.33}$，最大剪应力发生在表面下 ${\displaystyle z\approx 0.49a}$ 位置。

两个相同半径的交叉圆柱体的接触

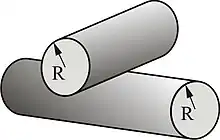
该接触等同于一个半径为 ${\displaystyle R}$ 的球体和一个平面的接触（见上）。

刚性圆柱体和弹性半空间的接触

一个刚性圆柱体压在一个弹性半空间上，产生的压力分布可写为[9]

${\displaystyle p=p_{0}\left(1-{\frac {r^{2}}{a^{2}}}\right)^{-1/2}}$ , 式中

${\displaystyle p_{0}={\frac {1}{\pi }}E^{*}{\frac {d}{a}}}$ .

凹痕的深度和法向力的关系可表述为

${\displaystyle F=2aE^{*}d{\frac {}{}}}$ .

刚性圆锥体和弹性半空间的接触

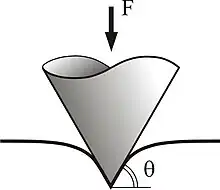
一个刚性圆锥体和一个弹性半空间作用时，压痕的深度和接触半径的关系为

${\displaystyle d={\frac {\pi }{2}}a\tan \theta }$ ,

式中 ${\displaystyle \theta }$ 为圆锥侧面和平面的夹角，则压力分布为

${\displaystyle p(r)=-{\frac {Ed}{\pi a\left(1-\nu ^{2}\right)}}ln\left({\frac {a}{r}}+{\sqrt {\left({\frac {a}{r}}\right)^{2}-1}}\right)}$ .

在圆锥顶尖应力有个对数奇点。总作用力为

${\displaystyle F_{N}={\frac {2}{\pi }}E{\frac {d^{2}}{\tan \theta }}}$ .

两个中心轴平行的圆柱体间的接触

两个中心轴平行的圆柱体接触时，作用力与压痕深度成线性比例关系：

${\displaystyle F={\frac {\pi }{4}}E^{*}Ld}$ .

次关系式曲率半径完全没有关系。接触半径可用通常的关系式来描述：

${\displaystyle a={\sqrt {Rd}}}$ ,

与两个球体的接触一样，式中

${\displaystyle {\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}$ ,

最大压力为

${\displaystyle p_{0}=\left({\frac {E^{*}F}{\pi LR}}\right)^{1/2}}$ .

球体和弹性半空间体的接触以及其一维替代模型

• 应变很小并在弹性范围内；
• 接触物体可以看作是弹性半空间体，也就是说，接触面远小于物体半径；
• 表面是连续的，不确定的 ；
• 表面无摩擦。

不满足这些条件的接触问题更加复杂，通常称之为非赫兹接触。

两个球体的接触。

无粘着接触的理论解可以按照接触面的几何形状分为两种。一种是确定性接触，变形发生前两个物体有多点接触。另一种是非确定性接触，两个接触物体的形状完全不同，以至于在零载荷下，它们只有一个点或一条线接触。在非确定性接触中，接触面积跟物体的尺寸相比，要小很多，而且该接触面的应力非常大。 对于线弹性材料接触，通常采用的方法是叠加，将不同接触点的解直接相加。比如半空间体的加载问题，通常将Flamant解作为起始点，然后产生不同形状的接触面。两个物体间的力平衡和力矩平衡作为附加约束再来求解。