散布圖
散点图(scatter plot、scatterplot、scatter graph、scatter chart、scattergram或scatter diagram)[3]是用笛卡尔坐标系上的點表示資料中二個或多個變數分佈方式的圖(例如班上同學的身高及體重)。多半是在平面笛卡尔坐标上,表示二個變數的分佈,若點有區分不同的顏色/形狀/大小,可以用此特性表示另一個變數。
| 散布圖 | |
|---|---|
 | |
| 品管七大手法之一 | |
| 首次使用 | 約翰·赫歇爾[1] |
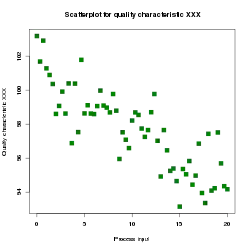
| 目的 | 確認兩個量化變量之間是否有相關性 |
散点图中的資料會用許多的點來表示,每個點表示一個資料,而其在水平座標軸及垂直座標軸上的座標,分別對應該資料的變數[4]。
簡介
散点图可以用來表示實驗中的連續自變量和另一個連續因变量之間的關係,也可以用來表示二個連續自变量之間的關係。若系統中存在參數,在實驗中會刻意增加或減少其數值,此參數即為自变量,若是自變量和因变量的散点图,一般會將自變量放在橫軸,因变量放在縱軸。若兩個參數都是自变量,可將任一個放在橫軸,此時,散点图可以看出其相關性的程度(但不一定是因果关系)。
散点图可以推測二個參數中許多不同種類的相關性,配合一定的置信区间。以體重及身高為例,可能會將體重放在y軸,將身高放在x軸。相關性可能是正相關(一參數增加時,另一參數對應增加)、負相關(一參數增加時,另一參數對應減少)、無相關性。若散点图有從左下到右上分佈的圖形,表示兩者正相關,若散点图有從左上到右下分佈的圖形,表示兩者負相關。為了研究兩參數之間的關係,可以在散点图上繪製擬合線(最適曲線、或趨勢線)。趨勢線的方程式就是參數相關性的方程式。若是線性相關,繪製最適曲線的程序即為線性回歸,保證在有限時間內有正確的解。針對任意的相關性關係,不存在通用、可以產生正確解的最適曲線產生程序。若是要確認兩組參數之間是否有非線性的關係,也可以用散点图來觀察。可以在散点图中加上平滑曲線(例如LOESS)來達到此一機能[5]。若數據可以表示為簡單關係的混合模型表示,其關係在視覺上上會是以疊加模式來表示。
例子
例如,為了要找到人肺容量以及其閉氣時間之間的關連性,研究者找了一群人進行研究,量測肺容量(第一個變量)及可以閉氣的時間(第二個變量),接著就可以畫散布圖,以肺容量為橫軸,閉氣的時間為縱軸。
若有一個人其肺容量是400 cl,可以閉氣21.7秒,則此數據會表示為座標(400, 21.7)的點,將所有人的資料都畫在一張圖上,可以讓研究者判斷兩個變量之間的關係。
散布圖矩陣
針對一組(超過二個)的資料變量X1, X2, ... , Xk,可以用散布圖矩陣(scatter plot matrix)畫出兩兩變量之間的散布圖,而多個散布圖以矩陣的形式放在同一個大圖中。散布圖矩陣會有k欄k列的方陣。其中每一個元素都是對應二個變量之間的散布圖[8]。每一欄和每一列都是一個維度,而矩陣中的每一個元素都是二維下的散布圖。
通用散布圖矩陣(generalized scatter plot matrix)[9]提供各種變量(量化變量以及分類變量)之間的成對關係。馬賽克圖、波動圖或多面條形圖可以表示兩個分類變量之間的關係。也有其他的圖可以說明量化變量以及分類變量之間的關係。

參考資料
- Friendly, Michael; Denis, Dan. . Journal of the History of the Behavioral Sciences. 2005, 41 (2): 103–130. PMID 15812820. doi:10.1002/jhbs.20078.
- Visualizations that have been created with VisIt (页面存档备份,存于) at wci.llnl.gov. Last updated: 2007-11-08.
- Jarrell, Stephen B. Special pre-publication. Dubuque, Iowa: Wm. C. Brown Pub. 1994: 492. ISBN 978-0-697-21595-6.
When we search for a relationship between two quantitative variables, a standard graph of the available data pairs (X,Y), called a scatter diagram, frequently helps...
- Utts, Jessica M. Seeing Through Statistics 3rd Edition, Thomson Brooks/Cole, 2005, pp 166-167. ISBN 0-534-39402-7
- Cleveland, William. . Murray Hill, N.J. Summit, N.J: At & T Bell Laboratories Published by Hobart Press. 1993. ISBN 978-0963488404.
- Nancy R. Tague. . The Quality Toolbox. Milwaukee, Wisconsin: American Society for Quality: 15. 2004 [2010-02-05]. (原始内容存档于2018-10-31).
- . AnyChart. [2016-02-03]. (原始内容存档于2016-02-01).
- Scatter Plot Matrix (页面存档备份,存于) at itl.nist.gov.
- Emerson, John W.; Green, Walton A.; Schoerke, Barret; Crowley, Jason. . Journal of Computational and Graphical Statistics. 2013, 22 (1): 79–91. doi:10.1080/10618600.2012.694762.
外部連結
| 维基共享资源上的相关多媒体资源:散布圖 |
- What is a scatterplot? (页面存档备份,存于)
- Correlation scatter-plot matrix for ordered-categorical data (页面存档备份,存于) – Explanation and R code
- Density scatterplot for large datasets (页面存档备份,存于) (hundreds of millions of points)
