星系型態分類
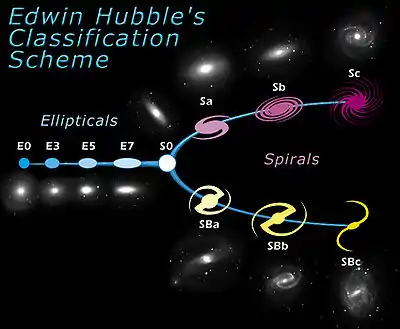
哈伯序列

哈伯序列是愛德溫·哈伯依據星系的外觀,在1926年發明的星系型態分類法[2][3]。因為傳統的圖說形狀像一把音叉,所以通常稱它是"哈伯音叉"。哈伯根據觀察所見的星系外觀(最初在攝影乾版上的影像),將星系劃分成三大類:
- 橢圓星系:有平滑、無特徵的光分佈,並且呈現橢圓的影像。它們用字母"E"表示,後面再跟隨一個整數,表示它們在天空中的橢圓度。
- 螺旋星系:由一個扁平的盤面組成,並有恆星組成螺旋臂的結構(通常是兩條旋臂),在中心有被稱為核球的隆起,是由高度密集的恆星組成。在外觀上類似橢圓星系;他們以字母"S"表示。大約有一半的旋臂被觀察到有像棒狀的結構從中心的核球延伸,這些被稱為棒旋星系,以字母"SB"表示。
- 透鏡星系:有一個明亮的中心核球被擴展的盤狀結構包圍著,但是透鏡星系的盤面沒有螺旋的結構,並且沒有活躍和明顯的恆星形成現象,這是與螺旋星系不同之處。它們以字母"S0"表示。

廣泛擴充這些類別之後,可以更好的區分外觀並涵蓋更多其它類型的星系。例如,沒有明顯結構(盤面或橢球形狀)的不規則星系。
哈伯序列通常以雙管齊下的叉子形式呈現,橢圓星系在左側,橢圓度從左向右增加;右端分岔形成兩根平行的帶狀,分別是螺旋星系和棒旋星系。透鏡星系被放置在橢圓星系和螺旋星系之間,相當於音叉的手柄和尖端分岔交會之處。
直到今天,無論是專業的天文研究還是業餘天文學,哈伯序列都還是最常用的分類法。
| 星系種類 | 質量(太陽質量) | 亮度(太陽亮度) | 直徑(千秒差距) | 恆星族群 | 觀測數量(%) |
|---|---|---|---|---|---|
| 螺旋/ 棒旋 |
109 to 1011 | 108 to 1010 | 5-250 | 盤面:星族I 暈:星族II |
77% |
| 橢圓 | 105 to 1013 | 105 to 1011 | 1-205 | 星族II | 20% |
| 不規則 | 108 to 1010 | 107 to 109 | 1-10 | 星族I | 3% |
哈伯序列是建立在由當時的望遠鏡所所拍攝的星系照片上。起初,他相信橢圓星系是早期的星系型態,然後可能轉變成螺旋或棒旋星系。我們現在則認為該倒過來解釋星系的發展。但是,早期的錯誤已經深植在天文學家的專業術語中,所以現在依然根據圖中的位置,將左邊的星系稱為早期形,圖右邊的稱為晚期形。
近代的觀測為我們提供更多關於這些星系類型的資訊:
- 橢圓星系的氣體和塵埃含量一般都很低,並且主要由老年的恆星組成。
- 螺旋星系一般有充足的氣體和塵埃,並且廣泛的有老年和年輕恆星的組合。
- 不規則星系含有相當豐富的氣體、塵埃和年輕的恆星。
據此,天文學家建構了一個星系演化的理論。建議橢圓星系,事實上,是螺旋星系和不規則星系彼此之間相互碰撞的結果,這種碰撞剝奪了大部分的氣體和塵埃,並使恆星的軌道呈現隨機化。參見星系的形成和演化。
| 名稱 | 赤經 | 赤緯 | 哈伯序列 |
|---|---|---|---|
| M49(NGC 4472) | 12h 29.8m | 8° 00' | E4 |
| M59(NGC 4621) | 12h 42.0m | 11° 39' | E3 |
| M60(NGC 4649) | 12h 43.7m | 11° 33' | E1 |
| M84(NGC 4374) | 12h 25.1m | 12° 53' | E1 |
| M86(NGC 4406) | 12h 26.2m | 12° 57' | E3 |
| M89(NGC 4552) | 12h 35.7m | 12° 33' | E0 |
| M110(NGC 205) | 00h 40.4m | 41° 41' | E6 |
佛科留斯系統

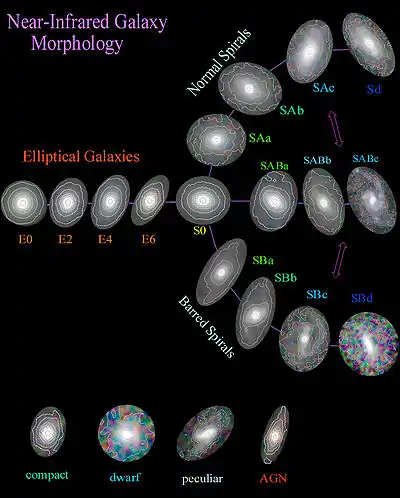



這個系統最早是在1959年由熱拉爾·佛科留斯提出,它是被廣泛使用的哈伯序列擴充,稱為佛科留斯系統[5]。佛科留斯認為哈伯對螺旋星系的二維分類只基於核球和螺旋臂的緊密,以及棒狀結構的是否存在,並沒有充分的描述觀測到的星系全部範圍的型態。特別是,他認為環和透鏡是組成螺旋星系的重要結構部分[6]。
佛科留斯系統保留了哈伯的基本星系型態,劃分成橢圓、透鏡、螺旋和不規則星系。為了補充哈伯的分類,佛科留斯根據三個形態特徵,引入了一個更複雜的螺旋星系分類系統:
- 棒:根據星系是否存在核棒來劃分。佛科留斯引入"SA"來表示沒有核棒的螺旋星系,以對應哈伯使用"SB"來表示棒渦星系。他還增加了中間類型的"SAB",表示核棒微弱(不明顯)的螺旋星系[7]。透鏡星系也被歸類為無核棒的(SA0)或有核棒的(SB0), (S0)保留給那些難以判斷核棒是否存在的星系(通常是因為它們是以側面朝向我們)。
- 環:分為有環狀結構的星系(符號為"(r)")和沒有環的星系(符號為"(s)") ,被賦予"(rs)"的是所謂"過渡"中的星系[7]。
- 螺旋臂:與哈伯最先的規劃一樣,主要是依據螺旋臂的緊密性來分類。佛科留斯擴展了哈伯的音叉臂,額外增加了幾個螺旋臂分類:
在哈伯最初的分類中,這三種類型的大多數星系都被歸類為不規則星系。此外,sd還包括哈伯的Sc類的一些星系。在Sm和Im類型中的星系分別是麥哲倫的螺旋和不規則星系,是依據麥哲倫雲命名的。大麥哲倫雲是SBm型,而小麥哲倫雲是不規則星系(Im)。
- Sd (SBd) – 中央核球非常微弱,由單獨的恆星集團和星雲組成破碎、漫反射的螺旋臂。
- Sm (SBm) – 外觀不規則;沒有核球的元件。
- Im – 螺旋臂極度不規則的星系。
分類法中不同的元素組合在一起 -按照列出的順序- 給出一個星系的完整分類。例如,一個核棒微弱和螺旋臂與環鬆散的螺旋星系的分類被表示為SAB(r)c。
在視覺上,佛科留斯系統可以看成是哈伯音叉的三維版本 (页面存档备份,存于)。在X軸上有階段(螺旋度),在Y軸上有家族(核棒),Z軸上有各種的環[8]。
數值哈伯級
佛科留斯還在他的分類法中為每一類星系指定了數值。哈伯分類為T,數值從-6到+10,負數對應於早期型的星系(橢圓星系和透鏡星系),正數對應於晚期型星系(螺旋星系和不規則星系)。橢圓星系分為三個"階段":緊湊型橢圓星系(cE)、普通橢圓星系E和晚期橢圓星系(E+)。透鏡星系就簡單的分為早期(S−)、中間(S0)和晚期(S+)類型。不規則星系可以分為麥哲倫不規則型(T = 10)或"緊湊型" ("T" = 11)。
| 哈伯級 T | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 佛科留斯分類[8] | cE | E | E+ | S0− | S00 | S0+ | S0/a | Sa | Sab | Sb | Sbc | Sc | Scd | Sd | Sdm | Sm | Im | |
| 近似哈伯分類[9] | E | S0 | S0/a | Sa | Sa-b | Sb | Sb-c | Sc | Sc-Irr | Irr I | ||||||||
數值級的使用可以對星系型態的分類進行更多的定量研究。
耶基斯(或摩根)分類
美國天文學家威廉·威爾遜·摩根與菲力浦·基南共同創建了以光譜對恆星分類的MMK分類法。耶基斯系統使用星系中恆星的光譜、形狀、實質和外觀、以及中心的凝聚度來分類星系。
| 光譜類型 | 注釋 |
|---|---|
| a | 顯著的A恆星 |
| af | 顯著的A-F恆星 |
| f | 顯著的F恆星 |
| fg | 顯著的F-G恆星 |
| g | 顯著的G恆星 |
| gk | 顯著的G-K恆星 |
| k | 顯著的K恆星 |
| 星系形狀 | 注釋 |
|---|---|
| B | 棒旋星系 |
| D | 對稱的旋轉沒有顯著的螺旋或橢圓結構 |
| E | 橢圓的 |
| Ep | 橢圓和塵埃吸收 |
| I | 不規則 |
| L | 表面亮度低 |
| N | 小而亮的核心 |
| S | 螺旋 |
| 傾斜度 | 注釋 |
|---|---|
| 1 | "正對"的星系 |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | "側面"的星系 |
所以,舉例如下:仙女座星系的分類為kS5。
相關條目
參考資料
- . www.spacetelescope.org. [27 February 2017]. (原始内容存档于2019-12-02).
- Hubble, E. P. . Contributions from the Mount Wilson Observatory / Carnegie Institution of Washington. 1926, 324: 1–49. Bibcode:1926CMWCI.324....1H.
- Hubble, E. P. . New Haven: Yale University Press. 1936. LCCN 36018182.
- . ESA/Hubble Press Release. [20 August 2013]. (原始内容存档于2020-11-24).
- De Vaucouleurs, G. . Handbuch der Physik. 1959, 53: 275. Bibcode:1959HDP....53..275D.
- Binney, J.; Merrifield, M. . Princeton: Princeton University Press. 1998. ISBN 978-0-691-02565-0.
- de Vaucouleurs, Gérard. . Astrophysical Journal Supplement. April 1963, 8: 31. Bibcode:1963ApJS....8...31D. doi:10.1086/190084.
- De Vaucouleurs, G. . 1994 [2008-01-02]. (原始内容 (PostScript)存档于2020-05-28).
- Binney, J.; Merrifield, M. . Princeton: Princeton University Press. 1998. ISBN 978-0-691-02565-0.
外部連結
- 星系和宇宙 (页面存档备份,存于) – 星系分類簡介(英文)
- 近紅外線星系型態圖 Archive.is的存檔,存档日期2012-08-02, T.H. Jarrett
- The Spitzer Infrared Nearby Galaxies Survey (SINGS) Hubble Tuning-Fork, SINGS Spitzer Space Telescope Legacy Science Project
- 前往星系動物園 (页面存档备份,存于) to try your hand at classifying galaxies as part of an Oxford University open community project