有界函数

在数学中，如果在某个集合${\displaystyle X}$上定义的具有实数或复数值的某个函数${\displaystyle f}$的值域是有界集合，则函数${\displaystyle f}$被称为有界的（或有界函数）。换句话说，存在实数${\displaystyle M>0}$，使得对于集合${\displaystyle X}$中的所有${\displaystyle x}$，都有${\displaystyle |f(x)|\leq M}$。有时，如果对于集合${\displaystyle X}$中的所有${\displaystyle x}$，都有${\displaystyle f(x)\leq A}$，则函数${\displaystyle f}$称为上有界的，${\displaystyle A}$就是它的一个上界；如果对于集合${\displaystyle X}$中的所有${\displaystyle x}$，都有${\displaystyle f(x)\geq B}$，则函数称为下有界的，${\displaystyle B}$就是它的一个下界。

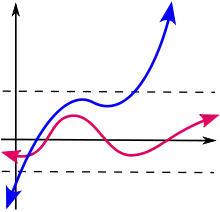
有界函数（红色）和无界函数（蓝色）的示意图。可以看到，有界函数的图形保持在（虚线）水平带内，而无界函数的图形不保持在水平带内。

一个特例是有界数列，其中${\displaystyle X}$是所有自然数所组成的集合${\displaystyle \mathbb {N} }$。所以，一个数列${\displaystyle f=(a_{0},a_{1},a_{2},\ldots )}$ 是有界的，如果存在一个数${\displaystyle M>0}$，使得对于所有的自然数${\displaystyle n}$，都有${\displaystyle \left\vert a_{n}\right\vert \leq M}$。