柯西序列
在数学中,柯西序列、柯西列、柯西数列(英語:),也称为基本列,是指一个元素随着序数的增加而愈发靠近的数列,[註 1]以数学家奥古斯丁·路易·柯西的名字命名。
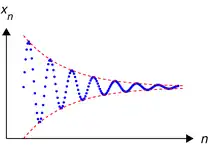
一个柯西序列 的绘图,使用蓝色, 相对于 。如果包含这个序列的空间是完备的,则这个序列的“最终目标”也就是极限存在
非柯西的一个序列。这个序列的元素不能随着序列前进而相互靠近
柯西列的定义依赖于距离的定义,所以只有在度量空间中柯西列才有意义。在更一般的一致空间中,可以定义更为抽象的柯西滤子和柯西网。
柯西列一个重要性质是,在完备空间中,所有的柯西数列都有极限且极限在这空间里,这就让人们可以在不求出这个极限(如果存在)的情况下,利用柯西列的判别法则证明该数列的极限是存在的。柯西列在构造具有完备性的代数结构的过程中也有重要价值,如构造实数。
度量空间中的柯西列
为了将柯西列的定义推广到一般的度量空间,必须将绝对值替换为该度量空间中的距离。
形式上说,给定任何一个度量空间,一个序列
被称为柯西列,如果对于任何正实数,存在一个正整数使得对于所有的整数,都有
其中表示和之间的距离。
直观上说,一个序列中的元素越来越靠近似乎说明这个序列必然在这个度量空间存在一个极限,而事实上在某些情况下这个结论是不对的。
完备性
一个度量空间中的所有柯西數列都會收斂到 中的一點 ,那么被称为是一个完备空间。
- 例子:实数
实数是完备的,而且标准的实数构造包含有理数的柯西列。
- 反例:有理数
有理数在通常定义的距离意义下不是完备的:
存在某个由有理数组成的序列,收敛到某个无理数,所以這數列在有理数這空間是不收敛的。
例如:
- 如下定义的序列:,即。可以证明这个序列收敛到一个无理数。
- 对于每个给定的而言,以下函数的值都可以表示为一个有理数序列的极限,但当为有理数时,这个值却是无理数。
推广
注释
- 更确切地说,在去掉有限个元素后,可以使得余下的元素中任何两点间的距离的最大值不超过任意给定的正数。
参考书目
- Lang, Serge. 3rd ed., reprint w/ corr. Addison-Wesley. 1997. ISBN 978-0-201-55540-0.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.