核主成分分析

线性PCA对于中心化后的数据进行分析，即

${\displaystyle {\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}=\mathbf {0} }$,

其中${\displaystyle \mathbf {x} _{i}}$是${\displaystyle N}$个多变量样本之一。之后将协方差矩阵

${\displaystyle C={\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}\mathbf {x} _{i}^{\top }}$

对角化。换言之，即是对协方差矩阵进行特征分解

${\displaystyle \lambda \mathbf {v} =C\mathbf {v} }$

或写作

${\displaystyle \lambda \mathbf {x} _{i}^{\top }\mathbf {v} =\mathbf {x} _{i}^{\top }C\mathbf {v} \quad \forall i\in [1,N]}$.[2]

一般而言，N个数据点在${\displaystyle d<N}$维空间中是线性不可分的，但它们在${\displaystyle d\geq N}$维空间中则是几乎必然线性可分的。这也意味着，如果我们能将N个数据点${\displaystyle \mathbf {x} _{i}}$映射到一个N维空间

${\displaystyle \Phi (\mathbf {x} _{i})}$ 其中 ${\displaystyle \Phi$ :\mathbb {R} ^{d}\to \mathbb {R} ^{N}}

中，就能很容易地构建一个超平面将数据点作任意聚类。不过由于经${\displaystyle \Phi }$映射后的向量是线性无关的，我们无法再像在线性PCA中那样显式地对协方差进行特征分解。

而在核PCA中，我们能够使用任意非平凡的函数${\displaystyle \Phi }$，但无需显式地计算在高维空间中的值，使我们得以使用非常高维的${\displaystyle \Phi }$。为了避免直接在${\displaystyle \Phi }$-空间（即特征空间）中操作，我们可以定义一个${\displaystyle N\times N}$的核

${\displaystyle K=k(\mathbf {x} ,\mathbf {y} )=(\Phi (\mathbf {x} ),\Phi (\mathbf {y} ))=\Phi (\mathbf {x} )^{T}\Phi (\mathbf {y} )}$

来代表特征空间的内积空间（见格拉姆矩阵）。这一对偶形式使我们能够进行主成分分析，同时又不用直接在${\displaystyle \Phi }$-空间中解协方差矩阵的特征值与特征向量。K中每一列的N个元素代表了转换后的一个数据点与所有N个数据点的点积。

由于我们并不在特征空间中进行计算，核PCA方法不直接计算主成分，而是计算数据点在这些主成分上的投影。特征空间中的一点在第k个主成分${\displaystyle V^{k}}$上的投影为

${\displaystyle {\mathbf {V} ^{k}}^{T}\Phi (\mathbf {x} )=\left(\sum _{i=1}^{N}\mathbf {a_{i}} ^{k}\Phi (\mathbf {x_{i}} )\right)^{T}\Phi (\mathbf {x} )}$

其中${\displaystyle \Phi (\mathbf {x_{i}} )^{T}\Phi (\mathbf {x} )}$代表点积，即核${\displaystyle K}$中的元素。上式中剩下的部分${\displaystyle \mathbf {a_{i}} ^{k}}$可以通过解特征方程

${\displaystyle N\lambda \mathbf {a} =K\mathbf {a} }$

得到，其中N为数据点的数量，${\displaystyle \lambda }$与${\displaystyle \mathbf {a} }$则分别为${\displaystyle K}$的特征值与特征向量。为了归一化${\displaystyle \mathbf {a} ^{k}}$，我们要求

${\displaystyle 1=(\mathbf {V} ^{k})^{T}\mathbf {V} ^{k}}$

值得注意的是，无论是否在原空间中对${\displaystyle x}$中心化，我们无法保证数据在特征空间中是中心化的。由于PCA要求对数据中心化，我们可以对K“中心化”：

${\displaystyle K'=K-\mathbf {1_{N}} K-K\mathbf {1_{N}} +\mathbf {1_{N}} K\mathbf {1_{N}} }$

其中${\displaystyle \mathbf {1_{N}} }$代表一个每个元素值皆为${\displaystyle 1/N}$的${\displaystyle N\times N}$矩阵。于是我们可以使用${\displaystyle K'}$进行前述的核PCA计算。[2]

在使用核PCA时，还有一点值得注意。在线性PCA中，我们可以通过特征值的大小对特征向量进行排序，以度量每个主成分所能够解释的数据方差。这对于数据降维十分有用，而这一技巧也可以用在核PCA中。不过，在实践中有时会发现得到所有方差皆相同，这通常是源于错误选择了核的尺度。

在实践中，大数据集会使K变得很大，从而导致存储问题。一种解决方式是先对数据集聚类，然后再对每一类的均值进行核PCA计算。有时即便使用此种方法仍会导致相对很大的K，此时我们可以只计算K中最大的P个特征值及相对应的特征向量。

应用核PCA前的数据点

使用核${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}}$进行核PCA分析后的数据点

使用高斯核进行核PCA分析后的数据点

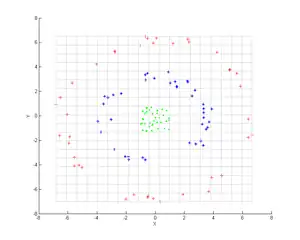
考虑图中所示的三组同心点云，我们试图使用核PCA识别这三组。图中各点的颜色并不是算法的一部分，仅用于展示各组数据点在变换前后的位置。

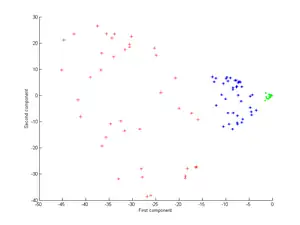
首先，我们使用核

${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}}$

进行核PCA处理，得到的结果如第二张图所示。

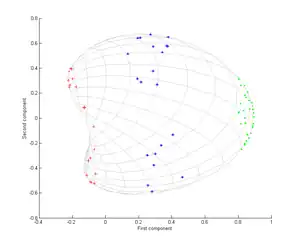
其次，我们再使用高斯核

${\displaystyle k({\boldsymbol {x}},{\boldsymbol {y}})=e^{\frac {-||{\boldsymbol {x}}-{\boldsymbol {y}}||^{2}}{2\sigma ^{2}}},}$

该核是数据接近程度的一种度量，当数据点重合时为1，而当数据点相距无限远时则为0。结果为第三张图所示。

此时我们注意到，仅通过第一主成分就可以区别这三组数据点。而这对于线性PCA而言是不可实现的，因而线性PCA只能在给定维（此处为二维）空间中操作，而此时同心点云是线性不可分的。

核PCA方法还可用于新奇检测（novelty detection）[3]与数据降噪[4]等。