隸屬函數

針對集合${\displaystyle X}$，集合${\displaystyle X}$上的隸屬函數是將集合${\displaystyle X}$映射到單位實數區間${\displaystyle [0,1]}$的函數。

${\displaystyle X}$集合上的隸屬函數對應${\displaystyle X}$集合中的模糊子集。對應模糊集合${\displaystyle {\tilde {A}}}$的隸屬函數一般會用${\displaystyle \mu _{A}}$來表示。針對集合中的元素${\displaystyle X}$，${\displaystyle \mu _{A}(x)}$的數值稱為${\displaystyle x}$對應模糊集合${\displaystyle {\tilde {A}}}$的隸屬度，表示符合模糊集合${\displaystyle {\tilde {A}}}$的程度。0表示元素${\displaystyle x}$不是模糊集合的元素，1表示元素${\displaystyle x}$是模糊集合的元素，0到1之間的值表示此元素部份符合模糊集合。

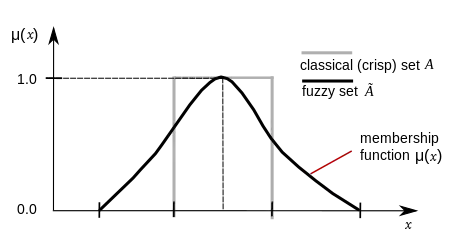
有時[2]會用一個更通用的定義，隸屬函數的值可以是任意的固定代數或是数学结构中取值${\displaystyle L}$，一般會要求${\displaystyle L}$至少是偏序关系或是格 (数学)。一般值在[0, 1]之間的隸屬函數此時會稱為[0, 1]-值隸屬函數。

隸屬函數的一個應用是在決策理論中的容度（capacity）。

在決策理論中，容度定義為函數${\displaystyle \nu }$，其定義域S是某個集合的子集，值域為${\displaystyle [0,1]}$，函數${\displaystyle \nu }$滿足集合定義上的單調而且正規化（也就是${\displaystyle \nu (\emptyset )=0,\nu (\Omega )=1}$）。這是廣義的機率量測，其中可數可加性的概率公理不一定要成立。容度用來表示某一事件可能性的量測，而特定結果下，其容度的期望值可以對容度作Choquet積分求得。

• 去模糊化
• 模糊量測理論
• 模糊集合運算
• 粗集合
• 模糊控制

• Zadeh L.A., 1965, "Fuzzy sets". Information and Control 8: 338–353.
• Goguen J.A, 1967, "L-fuzzy sets". Journal of Mathematical Analysis and Applications 18: 145–174