氦原子散射
氦原子散射(英語:, HAS)是材料學所使用的一種表面分析技術,透過測量由單色氦原子束入射到樣品上所造成的繞射粒子,來得知某材料的表面結構與晶格動力。
歷史
史上第一個氦原子散射實驗是由Estermann與Stern[1]在1930年於氟化鋰的晶面上所完成,這項實驗確立了當原子的物質波λ與原子間距在同個數量級,原子的繞射具有可行性。在當時,實驗的解析度受到氦原子束的大範圍速度分布所限制。直到1970年代時,技術發展使高強度的單色氦原子束能夠被製造出來,HAS探測表面結構的能力才得到廣泛的關注。 在當時,航空學及太空相關的問題幫助了許多稀薄空氣與固體表面碰撞的研究。1970年代,許多研究都利用氦原子散射找到材料繞射圖騰的精細結構。然而要直到1980年代左右,第三代噴嘴的發展,有關於表面聲子的研究才得以進行。這些噴嘴可以製造差距小於1meV的氦原子束,使固體表面震動模式與氦原子的非彈性碰撞,所產生的能量變化能夠被解析出來。因此,氦原子散射現可被用於探測材料的晶格動力。 第一個表面聲子的色散曲線紀錄於1981年[2],使人們在表面動力學的領域,對於氦原子散射的應用重新產生了興趣。
基本原理
表面靈敏度
普遍來說,表面鍵結有別於材料內鍵結,為了更精確建模與描述材料表面的性質,了解表面鍵結的特殊機制是必要的。為此必須使用一項技術只去探測材料的表面,稱為「表面靈敏度」,其中「觀察」粒子(無論是電子、中子或是原子)需要只「看」到表面(從表面收集資訊)。如果粒子過於深入樣品,那麼偵測到的就不只在於表面,連帶材料內部也會被偵測到。 雖然現行有幾種方式去探測材料的前幾個原子層,像是低能電子繞射(英語:, LEED)。但氦原子散射的特別之處在於它並不會穿透樣品的表面,事實上氦原子散射的「迴轉點」是在表面原子上方約3-4埃處。因此,它所攜帶的資訊就只包含樣品的極表層。 氦原子散射與電子散射的比較示意圖如下:
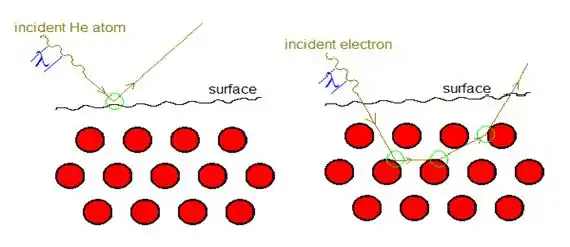
具熱能的氦氣,能像是在硬勢壁上的散射一般被建模起來,此時每個散射點都代表著恆定的表面電子密度。因為一個散射點就決定了氦原子與材料表面的交互作用,收集氦原子就能輕易地獲得材料表面結構的資訊,而無需考慮複雜得多電子繞射情形(例如低能電子繞射的情況)。
散射機制
入射氦原子與樣品表面原子的定性一維彈性相互作用位能如下:
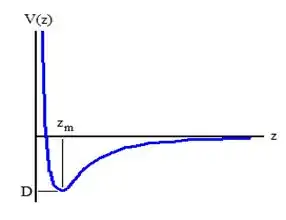
這位能可以分解為吸引與排斥,吸引部份是由於凡得瓦力,在較大的相對距離下占主導地位,而排斥部份是由於正電所產生的靜電造成,在較近的距離下有主導的地位。為了修正二維明面下的位能,添加一個函數來描述樣品的表面原子波紋。造成的三維位能能夠以波狀的莫爾斯勢來建模而成,如下[3]:
函數第一項是橫向的平均表面位能——一個深度為D的位能井,最小值z = zm 與一個擬合參數 α。而第二項是由波狀函數ξ(x,y)修改而成的排斥位能,具有和表面相同的週期性,以及一個擬合參數 β。
氦原子能夠以彈性(沒有能量移轉)散射,或是透過表面震動模式(聲子的創造與湮滅)激發與去激發來造成非彈性散射。兩者的散射結果皆可用於研究材料表面的性質。
為什麼使用氦原子?
相較於X射線、中子及電子去探測物體表面,使用氦原子在研究表面結構與聲子動力學上有一些優勢存在。如同先前提到過的,具熱能的氦原子不會穿透進去研究的材料中,這意味著除了對表面高度敏感,它們對樣品是完全不具破壞性的。氦原子的物質波與原子的間距在同個數量級,使其成為理想的探測粒子。也由於它們是中性粒子,氦原子對表面的電荷不具敏感性。作為高貴氣體,氦氣也具化學惰性。在一般情況下,氦原子是個惰性的探測物(化學上、電學上、磁力上與機械上都是),這使他能夠用在廣泛的表面研究上,包含那些具放射性與半穩定狀態地材料上。氦原子可甚至探測含有電磁場或是在超高真空的表面上,而不會影響到其他正在進行的程序。因此,氦原子在測量濺鍍、退火與吸附層沉積上是相當有用的。 最後,由於有溫度的氦原子不具旋轉與震動的自由度,並且不會有電子的轉移,所以只需要分析入射束與散射束的動能轉移,就能得出測量表面的資訊。
器材
下圖是氦原子散射實驗普遍所採用的設置。包含了噴嘴束來源、含有晶體控制器的超高真空散射腔,與一個偵測室。每個系統都可能會有特殊的安排與設置,但多數都會有這些最基本的架構。
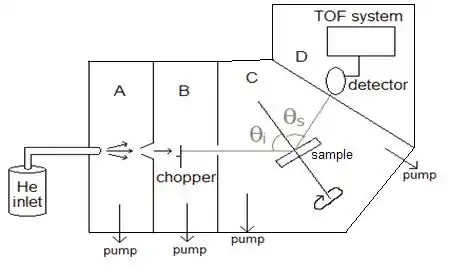
來源
能量分布小於1meV的氦原子束,是透過氦氣在壓力~200bar下絕熱自由膨脹,經過~5-10μm噴嘴[4]後進入低壓腔室中。根據系統的工作溫度的範圍,典型的氦原子能量可以是5-200meV。在A與B之間的錐形孔稱為溢流口,只讓氦原子光束的中心部分通過。此時,氦原子束的粒子應幾乎為等速度。另外在B部分有一個斬波系統,負責創造量測時間差所需要的脈衝,這等一下會談到。
散射腔
C部分散射腔通常包含了晶體控制器與任何量測晶體表面所需要的儀器,腔內的器材可包含LEED螢幕(對表面結構進行補充測量)、歐傑電子能譜儀(以決定表面的汙染等級)、質譜儀(監測真空品質與殘餘氣體的成分),以及為了金屬表面,需要一個離子槍以清洗樣品表面。為了保持乾淨的表面,散射腔的壓力須保持在10−8 到 10−9 Pa的範圍內。這需要使用渦輪分子幫捕或是低溫真空幫補才能達成。
晶體控制器
晶體控制器允許樣品實現至少三種運動模式,方位角旋轉能讓晶體改變表面原子的方向,傾斜角用於將晶體的法線設置為在散射平面中,而控制器繞z軸旋轉能改變氦原子束的入射角。晶體操縱器還應該包含一個系統來控制晶體的溫度。
偵測
氦原子束在晶體表面上散射後,跑去了D區域。最常使用的偵測器配置是一個電子轟擊離子源,然後是一個質量過濾器和一個電子倍增器。散射後的原子束經過一連串的微分泵級,使在到達偵測器前能夠將信噪比降低。時間差分析儀可以跟隨探測器測量能量的損失。
彈性測量
在彈性繞射主導下,繞射峰的相對角位置反映了測量表面的幾何性質。因此,峰值的位置接露了觀測到晶體表面的二維空間群的對稱性。峰值間的寬度顯示了氦原子束的速度分布。彈性散射由兩個運動學條件決定——能量守恆和平行於晶體動量分量的能量:
Ef = Ei => ki² = kG² = kGz² + k||G²
k||G = k||i + G
在此G是倒易晶格的向量,kG 和 ki 是最終與初始入射氦原子束的波向量。埃瓦爾德球的結構能夠使觀察到繞射氦原子束,並在出現時決定它的散射角。特徵繞射圖案將會出現,並由表面的周期性決定,類似於布拉格定律中所見的方式。 多數的氦原子散射研究會在由入射原子束方向和表面法線定義的平面中掃描探測器。將埃瓦爾德球縮小至半徑 R=k0 只與散射平面中的倒易晶格桿相交,如下所示:
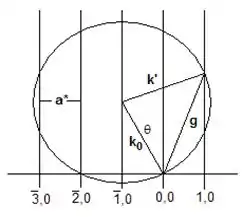
繞射峰的強度提供了靜態氣體與表面相互作用位能的訊息,量測不同入射氦原子束狀態下的的繞射峰強度,能夠得出表面電子密度,並得出最外層原子的皺褶排列型態。
值得注意的是偵測氦原子比偵測電子沒效率,所以散射密度一次只能於一個點在k-space中決定。在理想的平面上,繞射峰之間彈性散射強度應該為0,反之材料表面有階層或是吸附電子存在。從繞射峰角度的位置、寬度與強度來看,可以獲得表面結構、對稱性與特徵排列的訊息。
非彈性測量
非彈性HAS接露了材料上的聲子色散現象。在散射角遠離反射角與繞射角時,有序表面的散射強度由非彈性碰撞決定。
為了研究僅由單聲子所引起的氦原子束非彈性散射,需要對散射原子進行能量分析。最知名的方法莫過於利用時間差分析(, TOF),TOF需要氦原子束經過機械斬波器來製造脈衝,讓射往偵測器的原子束有「空間」進行時間差分析。非彈性散射的氦原子束會在遇到表面時失去些能量,因此速度相較於入射原子束會有所不同。透過散射粒子束強度的變化,聲子的創造與湮滅就可以被測量到。 透過改變散射角或是改變入射原子束的能量,能在不同的能量和動量傳遞值下對非彈性散射進行取樣,繪製出色散關係,並且由分析色散曲線可以得到表面結構和鍵結的資訊。一個TOF分析能夠顯示強度峰值與時間的關係。主要高峰(有最大的強度)是由未散射氦原子束所「包」住的,而左邊的高峰代表著聲子湮滅。如果發生了聲子的創造,則高峰會出現在右邊。
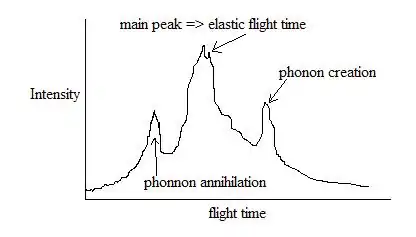
上面的定性圖顯示了TOF圖表在繞射角附近可能看起來的樣子。但是,隨著晶體旋轉遠離了繞射角,主要彈性高峰會劇烈的落下,不過由於表面缺陷所產生的不相關彈性散射,強度始終不會降至0,就算在遠離繞射角的情況下也是。因此,非相關彈性高峰的強度與其對散射角的依賴性,能夠提供晶體表面缺陷的資訊。
有關聲子創造與湮滅的運動學關係是相當簡單的,只要將能量守恆與以及動量相結合,就能得出能量交換ΔE與動量交換q在碰撞過程中的方程式。這項非彈性散射過程可被描述成,聲子的能量ΔE=ћω,以及波向量q。晶格的振動模式可由聲子頻率 ω 作為聲子波向量 q 的函數:ω(q)來描述而成。 除了偵測表面的聲子,由於氦原子束的低能量特性,它也可偵測吸附物的低頻震動,進而決定他們的位能。
參考文獻
- Estermann, I.; Stern, O. . Zeitschrift für Physik (Springer Science and Business Media LLC). 1930, 61 (1–2): 95–125. Bibcode:1930ZPhy...61...95E. ISSN 1434-6001. S2CID 121757478. doi:10.1007/bf01340293 (德语).
- Brusdeylins, G.; Doak, R. Bruce; Toennies, J. Peter. . Physical Review Letters (American Physical Society (APS)). 1981-02-09, 46 (6): 437–439. Bibcode:1981PhRvL..46..437B. ISSN 0031-9007. doi:10.1103/physrevlett.46.437.
- A brief introduction to helium atom scattering, University of Cambridge
- M.C. Desjonquéres, D. Spanjaard, Concepts in Surface Physics, Second Edition, Springer (1996)