波德靈敏度積分

波德靈敏度積分（Bode's sensitivity integral）是由亨德里克·韋德·波德所提出的公式，針對線性非時變回授控制系統的一些限制進行量化。回控控制系統會將輸出信號經由感測器回授進入系統，系統設計時，一方面希望實際輸出可以盡量接近理想輸出，另一方面也希望使系統盡量不受外部擾動的影響（降低系統對擾動靈敏度）。波德靈敏度積分是針對系統對擾動靈敏度進行量化。

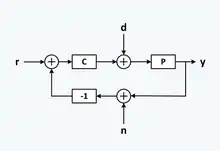
回授控制的方塊圖

圖中P是一個動態過程，傳遞函數是P(s)。控制器C的傳遞函數是C(s)。控制器設法讓過程輸出y追隨參數輸入r，但因為干擾d以及量測誤差n的存在，會讓輸出出現未預期的變化。

令L為迴路传递函数，也是迴路增益，L(s) = P(s)C(s)，而S為靈敏度函數，再針算靈敏度函數對數值對所有頻率下的積分，則下式會成立：

${\displaystyle \int _{0}^{\infty }\ln |S(j\omega )|d\omega =\int _{0}^{\infty }\ln \left|{\frac {1}{1+L(j\omega )}}\right|d\omega =\pi \sum Re(p_{k})-{\frac {\pi }{2}}\lim _{s\rightarrow \infty }sL(s)}$

其中${\displaystyle p_{k}}$為L在右半平面的極點（不穩定的極點）。

若L的极点比零点多二個或是二個以上，且沒有位在右半平面极点（所有極點都穩定），上式可以簡化為：

${\displaystyle \int _{0}^{\infty }\ln |S(j\omega )|d\omega =0}$

靈敏度越低越好，但由波德靈敏度積分可以看出，若在某一個頻率段降低擾動的靈敏度，因為波德靈敏度積分為定值，因此一定會有某一個頻率段的擾動靈敏度會因此而上昇，這稱為「水床效應」（waterbed effect）[1]。因此無法針對所有頻段降低系統靈敏度。