湯普森群
數學上，湯普森群（英語：）是理查德·湯普森1965年在幾份未發表的手寫筆記中，提出的三個群，通常記為F⊂T⊂V。這三個群中受到最廣泛研究的是群F。有時湯普森群單單指群F。
這三個湯普森群有許多不尋常性質，當中尤以F為甚，因此成為了群論中不少猜想的反例。這三個群都是有限展示的無限群。T和V是罕有的無限但為有限展示的單群。F不是單群，但其換位子群[F,F]是單群。F對換位子群的商F/[F,F]是秩2的自由阿貝爾群。F是全序群，有指數增長率，無子群同構於秩2自由群。
群F是否可均群的問題，爭議頗大，有兩方各執一端：E. Shavgulidze和Justin Moore各自發表預印論文，聲稱F是可均群；另外Azer Akhmedov和Leva Beklaryan也各自發表預印論文，聲稱F不是可均群。但是這些預印論文的證明隨後都發現有錯誤。至今難以猜測F是否可均群。[1]
現時已知F不是初等可均群，假如F不是可均群，則會成為有限展示群的馮紐曼猜想的另一個反例。這個猜想指有限展示的非可均群都有子群同構於秩2自由群，自提出後多年未解，直至2003年才被推翻。
Higman (1974)提出了一個以有限展示單群組成的無限族，湯普森群V是這個族中一個特例。
展示
群F的一個有限展示如下：
![{\displaystyle \langle A,B\mid \ [AB^{-1},A^{-1}BA]=[AB^{-1},A^{-2}BA^{2}]=\mathrm {id} \rangle }](../I/3aa741bdc915a1f7baea62d1f970a171b87b476a.svg)
其中[x,y]是換位子xyx−1y−1.
雖然F可表達為有兩個生成元及兩個關係元的有限展示，但用以下的無限展示較容易理解：
以上兩個展示間的關係為 x0=A, xn = A1−nBAn−1 對n>0。
其他表示
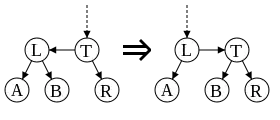
群F可以用有序有根的二元樹上的運作表示。群F也可以表達為單位區間上由所有如下所述的分段線性同胚組成的群：同胚保持區間的定向，不可微點都是二進有理數（即形為m/2n的數，其中m, n為整數），每段的斜率都是2的冪。
將單位區間的端點等同，便可以視群F為在單位圓上作用，而群T是在F中加入單位圓的同胚x→x+1/2 mod 1而生成的群。在二元樹上的對應操作是把根節點下方的兩棵樹交換。群V是在群T中加入一個不連續映射而生成的群，這映射固定半開區間[0,1/2)的點，並用最顯然的方法交換區間[1/2,3/4)和[3/4,1)。在二元樹上的對應操作為把根節點的右子節點下的兩棵樹（如有的話）交換。
參考
- . Mathoverflow. [2013-11-02]. （原始内容存档于2013-11-05）.
- Cannon, J. W.; Floyd, W. J.; Parry, W. R., (PDF), L'Enseignement Mathématique. Revue Internationale. IIe Série, 1996, 42 (3): 215–256 [2013-11-02], ISSN 0013-8584, MR 1426438, （原始内容存档 (PDF)于2013-05-12）
- Cannon, J.W.; Floyd, W.J. (PDF). Notices of the American Mathematical Society. September 2011, 58 (8): 1112–1113 [December 27, 2011]. ISSN 0002-9920. （原始内容存档 (PDF)于2013-11-04）.
- Higman, Graham, , Notes on Pure Mathematics 8, Department of Pure Mathematics, Department of Mathematics, I.A.S. Australian National University, Canberra, 1974 [2013-11-02], ISBN 978-0-7081-0300-5, MR0376874, （原始内容存档于2014-01-01）