球面三角學
球面上的線
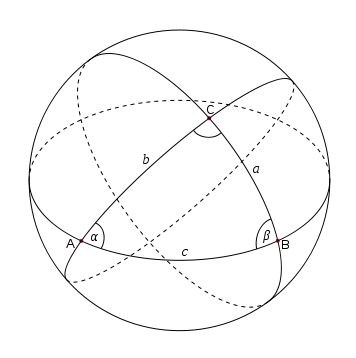
在球殼的表面,最短的距離是大圓上接近直線的弧線,也就是圓弧的圓心與球殼的球心是同一點。例如:地球上的子午線和赤道都是大圓。所謂行星表面的直線,就是球面上兩點之間最近距離的大圓弧線(如果把自己拘束在球面上的直線上)。
在球面上,由大圓的弧所包圍的區域稱為球面多邊形,但要注意,不同於平面上的情形,在球面上二角形是可能存在的。(兩個弧夾出兩個角的三角形類似物)
這些多邊形的邊長(弧長),可以利用球心角很方便的來測定,將弧的兩端所對應的球心角乘上半徑便是邊長。要注意的是,這些角都必須用弳度量來量度。.
因此,對一個球面三角形而言,是由他的弧長與球心角來具體描述的,只是弧的長度是用弳度量來標示。
值得注意的是,球面三角形的三個內角的和總是大於180°,但在平面上只有180°。超過180°的數值稱為球面剩餘 E:E = α + β + γ - 180°,這些結餘給出了球面三角形的面積。確定這個值,球面剩餘必須以弳度量來測定,表面積A依據球面的半徑和球面剩餘來測量:
- A = R2 · E
這是高斯-博內定理,這很明顯的顯示沒有相似的球面三角形(三角形有相同的角,但不同)。而在特殊的情況下,球的半徑為1,則球面三角形的面積A = E。
要解球面幾何的問題,要點是能剖析出其中的直角三角形(三個角中有一個是90°),因為這樣就可以利用納皮爾的多邊形求解。
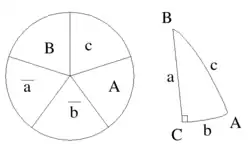
利用納皮爾多邊形(也稱為納皮爾圓周)的口訣可以很輕易的記住球面直角三角形的所有關聯性: 以他們出現於球面三角形的順序,依照相鄰的邊角關係,依序將三角形的六個角寫在一個圈子內,也就是開始以一個角度開始,然後在它旁邊寫上相鄰的邊的弧角度,繼續再寫下下一個角度,···,最後結束成一個圓。然後刪除90°的角角度并且將它相鄰的弧角度替換成他們補角的數值(與原角弧度之和為90°) (也就是將 a 換成 90° − a)。 現在,這五個數組成了我們需要的納皮爾多邊形(納皮爾圓周),從這兒,可以得到每個角度的餘弦值等於:
可以參考半正矢(Haversine formula),能在球面三角上解析弧長與角度,為航海學提供了穩定的模式。
恆等式
參見
- 球面幾何學
- 球面距離
- 大地測量學
外部連結
- 《基礎幾何學》:球面幾何和球面三角學(页面存档备份,存于)
- Wolfram's mathworld: Spherical Trigonometry(页面存档备份,存于) 更多的公式列表與一些推導
- Wolfram's mathworld: Spherical Triangle(页面存档备份,存于) nice applet
- Spherical Trigonometry — for the use of colleges and schools by I. Todhunter, M.A., F.R.S. Historical Math Monograph posted by Cornell University Library.
- 关于偏差平面和简单平面的说明书(页面存档备份,存于) 是阿拉伯语的历史可以追溯到1740年谈球面三角学,图的手稿。