離散小波變換

• 首先我們定義一些需要用到的信號及濾波器。
• x[n]：離散的輸入信號，長度為N。
• ${\displaystyle g[n]}$：low pass filter低通濾波器，可以將輸入信號的高頻部份濾掉而輸出低頻部份。
• ${\displaystyle h[n]}$：high pass filter高通濾波器，與低通濾波器相反，濾掉低頻部份而輸出高頻部份。
• ${\displaystyle \downarrow }$ Q：downsampling filter降采样濾波器，如果以x[n]作為输入，則輸出y[n]=x[Qn]。此處舉例Q=2。

舉例說明:

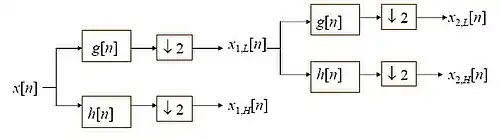
清楚規定以上符號之後，便可以利用階層架構來介紹如何將一個離散信號作離散小波轉換：

架構中的第1層(1st stage)

${\displaystyle x_{1,L}[n]=\sum _{k=0}^{K-1}x[2n-k]g[k]}$

${\displaystyle x_{1,H}[n]=\sum _{k=0}^{K-1}x[2n-k]h[k]}$

架構中的第2層(2nd stage)

${\displaystyle x_{2,L}[n]=\sum _{k=0}^{K-1}x_{1,L}[2n-k]g[k]}$

${\displaystyle x_{2,H}[n]=\sum _{k=0}^{K-1}x_{1,L}[2n-k]h[k]}$

可繼續延伸

${\displaystyle \vdots }$

${\displaystyle \vdots }$

架構中的第${\displaystyle \alpha }$層(${\displaystyle \alpha -th}$ stage)

${\displaystyle x_{\alpha ,L}[n]=\sum _{k=0}^{K-1}x_{\alpha -1,L}[2n-k]g[k]}$

${\displaystyle x_{\alpha ,H}[n]=\sum _{k=0}^{K-1}x_{\alpha -1,L}[2n-k]h[k]}$

注意：若輸入信號${\displaystyle x[n]}$的長度是N，則第${\displaystyle \alpha }$層中的${\displaystyle x_{\alpha ,L}[n]}$及${\displaystyle x_{\alpha ,H}[n]}$的長度為${\displaystyle {\frac {N}{2^{\alpha }}}}$

此時的輸入信號變成${\displaystyle x[m,n]}$，而轉換過程變得更複雜，說明如下：

首先對n方向作高通、低通以及降頻的處理

${\displaystyle v_{1,L}[m,n]=\sum _{k=0}^{K-1}x[m,2n-k]g[k]}$

${\displaystyle v_{1,H}[m,n]=\sum _{k=0}^{K-1}x[m,2n-k]h[k]}$

接著對${\displaystyle v_{1,L}[m,n]}$與${\displaystyle v_{1,H}[m,n]}$延著m方向作高低通及降頻動作

${\displaystyle x_{1,LL}[m,n]=\sum _{k=0}^{K-1}v_{1,L}[2m-k,n]g[k]}$

${\displaystyle x_{1,HL}[m,n]=\sum _{k=0}^{K-1}v_{1,L}[2m-k,n]h[k]}$

${\displaystyle x_{1,LH}[m,n]=\sum _{k=0}^{K-1}v_{1,H}[2m-k,n]g[k]}$

${\displaystyle x_{1,HH}[m,n]=\sum _{k=0}^{K-1}v_{1,H}[2m-k,n]h[k]}$

經過(1)(2)兩個步驟才算完成2-D DWT的一個stage。

以下根據上述2-D DWT的步驟，對一張影像作二維離散小波轉換(2D Discrete Wavelet Transform)

原始影像

2D DWT的結果

${\displaystyle \Rightarrow }$

在討論複雜度之前，先做一些定義，當x[n]*y[n]時，x[n]之長度為N，y[n]之長度為L： ${\displaystyle \ \Rightarrow IDFT_{N+L-1}\left[DFT_{N+L-1}(x[n])DFT_{N+L-1}(y[n])\right]}$

其中，

${\displaystyle \ IDFT_{N+L-1}}$為(N+L-1)點離散傅立葉反轉換(inverse discrete Fourier transform)

${\displaystyle \ DFT_{N+L-1}}$為(N+L-1)點離散傅立葉轉換(discrete Fourier transform)

(1)一維離散小波轉換之複雜度(沒有分段卷积(sectioned convolution))：

${\displaystyle {\frac {3}{2}}(N+L-1)\log _{2}{(N+L-1)}\approx {\frac {3}{2}}N\log _{2}N}$

(2)當 N >>> L 時，使用 “分段卷积(sectioned convolution)”的技巧：

將x[n]切成很多段，每段長度為${\displaystyle \mathbb {N} _{1}}$，總共會有${\displaystyle S={\frac {N}{N_{1}}}}$段，其中${\displaystyle N>N_{1}>>L}$。

則

${\displaystyle \ x[n]*g[n]=x_{1}[n]*g[n]+x_{2}[n]*g[n]+...+x_{s}[n]*g[n]}$

${\displaystyle \ x[n]*h[n]=x_{1}[n]*h[n]+x_{2}[n]*h[n]+...+x_{s}[n]*h[n]}$

複雜度為：

${\displaystyle {\begin{aligned}{\frac {3}{2}}S(N_{1}+L-1)\log _{2}{(N_{1}+L-1)}&\approx {\frac {3}{2}}SN_{1}\log _{2}(N_{1}+L-1)\\&\approx {\frac {3}{2}}N\log _{2}(N_{1}+L-1)\\&\approx {\frac {3}{2}}N\log _{2}N_{1}\\\end{aligned}}}$

在這裡要注意的是，當N>>L時，一維離散小波轉換之複雜度是呈線性的(隨N)，${\displaystyle {\mathit {O(N)}}}$。

(3)多層(Multiple stages )的情況下：

1.若${\displaystyle \ x_{a,H}[n]}$不再分解時：

${\displaystyle {\begin{aligned}Complexity&\approx \left(N+{\frac {N}{2}}+{\frac {N}{4}}+{\frac {N}{8}}+...+2\right){\frac {3}{2}}\log _{2}N_{1}\\&=(2N-2){\frac {3}{2}}\log _{2}N_{1}\\&\approx 3N\log _{2}N_{1}\\\end{aligned}}}$

2.若${\displaystyle \ x_{a,H}[n]}$也細分時：

${\displaystyle {\begin{aligned}Complexity&\approx \left(N+2{\frac {N}{2}}+4{\frac {N}{4}}+8{\frac {N}{8}}+...+{\frac {N}{2}}2\right){\frac {3}{2}}\log _{2}N_{1}\\&=(N\log _{2}N){\frac {3}{2}}\log _{2}N_{1}\\\end{aligned}}}$

(4)二維離散小波轉換之複雜度(沒有分段卷积(sectioned convolution))： ${\displaystyle \ \Rightarrow M{\frac {3}{2}}(N+L-1)\log _{2}{(N+L-1)}+(N+L-1){\frac {3}{2}}(M+L-1)\log _{2}{(M+L-1)}}$

上式中，第一部分需要M個一維離散小波轉換並且每個一維離散小波轉換的輸入有N個點；第二部分需要N+L-1個一維離散小波轉換並且每個一維離散小波轉換的輸入有M個點。

${\displaystyle {\begin{aligned}Complexity&\approx {\frac {3}{2}}MN\log _{2}N+{\frac {3}{2}}MN\log _{2}M\\&={\frac {3}{2}}MN(\log _{2}N+\log _{2}M)\\&={\frac {3}{2}}MN\log _{2}MN\\\end{aligned}}}$

(5)二維離散小波轉換之複雜度，使用 “分段卷积(sectioned convolution)”的技巧：

假設原始尺寸為${\displaystyle M\times N}$，則每一小部分的尺寸為${\displaystyle M_{1}\times N_{1}}$

${\displaystyle {\begin{aligned}Complexity&\approx {\frac {MN}{M_{1}N_{1}}}{\frac {3}{2}}M_{1}N_{1}\log _{2}M_{1}N_{1}\\&={\frac {3}{2}}MN\log _{2}M_{1}N_{1}\\\end{aligned}}}$

所以若是使用分段摺積，則二維離散小波轉換之複雜度是呈線性的(隨MN)，${\displaystyle {\mathit {O(MN)}}}$。

(6)多層(Multiple stages )與二維的情況下：

首先x[m,n]的尺寸為${\displaystyle M\times N}$，

1.若${\displaystyle \ x_{a,H_{1}}[n],x_{a,H_{2}}[n],x_{a,H_{3}}[n]}$不細分，只細分${\displaystyle \ x_{a,L}[n]}$時，總複雜度為：

${\displaystyle {\begin{aligned}totalcomplexity&=\left(MN+{\frac {MN}{4}}+{\frac {MN}{16}}+...\right){\frac {3}{2}}\log _{2}M_{1}N_{1}\\&\approx {\frac {4}{3}}MN{\frac {3}{2}}\log _{2}M_{1}N_{1}\\&=2MN\log _{2}M_{1}N_{1}\\\end{aligned}}}$

2.若${\displaystyle \ x_{a,H_{1}}[n],x_{a,H_{2}}[n],x_{a,H_{3}}[n]}$也細分時，總複雜度為：

${\displaystyle {\begin{aligned}totalcomplexity&=\left(MN+4{\frac {M}{2}}{\frac {N}{2}}+16{\frac {M}{4}}{\frac {N}{4}}+...\right){\frac {3}{2}}\log _{2}M_{1}N_{1}\\&=\left[MN\log _{2}(min(M,N))\right]{\frac {3}{2}}\log _{2}M_{1}N_{1}\\\end{aligned}}}$

使用離散小波轉換，將訊號個別通過一個低通濾波器和一個高通濾波器，得到訊號的高低頻成分，而在重建(Reconstruction)原始訊號的過程，也就是離散小波的逆轉換(Inverse Discrete Wavelet Transform. IDWT)，直觀而言，我們僅是需要將離散小波轉換做重建濾波即可得到原始輸入信號，以下將推導重建濾波器，也就是IDWT高低通濾波器的構成要件，以及如何來重建原始信號。

${\displaystyle X(z)=\sum x(n)z^{-n}}$

${\displaystyle X_{1,L}(z)={\frac {1}{2}}[X(z^{\frac {1}{2}})G(z^{\frac {1}{2}})+X(-z^{\frac {1}{2}})G(-z^{\frac {1}{2}})]}$

${\displaystyle X_{1,H}(z)={\frac {1}{2}}[X(z^{\frac {1}{2}})H(z^{\frac {1}{2}})+X(-z^{\frac {1}{2}})H(-z^{\frac {1}{2}})]}$

${\displaystyle X_{0}(z)={\tfrac {1}{2}}[X(z)G(z)+X(-z)G(-z)]G_{1}(z)+{\tfrac {1}{2}}[X(z)H(z)+X(-z)H(-z)]H_{1}(z)}$

${\displaystyle ={\tfrac {1}{2}}[G(z)G_{1}(z)+H(z)H_{1}(z)]X(z)+{\tfrac {1}{2}}[G(-z)G_{1}(z)+H(-z)H_{1}(z)]X(-z)}$

條件1：${\displaystyle G(z)G_{1}(z)+H(z)H_{1}(z)=2}$

條件2：${\displaystyle G(-z)G_{1}(z)+H(-z)H_{1}(z)=0}$

${\displaystyle {\binom {G_{1}(z)}{H_{1}(z)}}={\frac {2}{det(H_{m}(z))}}{\binom {H(-z)}{-G(-z)}}}$

其中 ${\displaystyle det(H_{m}(z))=G(z)H(-z)-H(z)G(-z)}$

壓縮、去除雜訊：使用低通濾波器，將小波轉換的高頻濾掉，即保留${\displaystyle x_{1,LL}[m,n]}$而將其他部分捨棄。

• 邊緣偵測：使用高通濾波器，將小波的低頻濾掉，即保留${\displaystyle x_{1,HL}[m,n]}$或${\displaystyle x_{1,LH}[m,n]}$而捨棄其他部分。
• R语言小波分析wavelet （页面存档备份，存于）
• 作為 JPEG2000 的內部架構
• 模式辨認：由於可以利用低頻的部分得到原圖的縮略版，加上模式通常為整體的特性，藉由在縮略圖上進行工作，小波轉換可以有效減少尋找模式與比對模式的運算時間
• 濾波器設計：小波轉換保留部分時間資訊，可以據此資訊加上訊號的強度資訊，保留特定時點的資訊而同時去除雜訊

• 小波分析
• 連續小波轉換
• 哈爾小波轉換
• 信號處理

• Jian-Jiun Ding, Time frequency analysis and wavelet transform class note,the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2009,2016 .http://djj.ee.ntu.edu.tw/TFW.htm （页面存档备份，存于）
• Stéphane Mallat, A Wavelet Tour of Signal Processing （页面存档备份，存于）