科恩系列分佈
科恩系列分佈(Cohen's class distribution)於1966年由L. Cohen首次提出,且其使用雙線性轉換亦是此種轉換形式中最通用的一種。在幾種常見的時頻分佈中,Cohen's class分佈是最強大的轉換之一。隨著近幾年來時頻分析發展,應用也越來越多元。Cohen's class分佈和短時距傅立葉變換比較起來有較高的清晰度,但也相對的有交叉項(cross-term)的問題,不過可選擇適當的遮罩函數(mask function)來將交叉項的問題降到最低。
數學定義
- ,
- 其中 為模糊函數(Ambiguity Function) ,且為一遮罩函數,通常是低通函數用來濾除雜訊。
科恩系列分佈函數
韋格納分布(Wigner Distribution Function)
- 當Cohen's class分佈中的時,Cohen's class分佈會成韋格納分布(Wigner distribution function)。
- 利用韋格納分佈對函數作時頻分析的結果可見右圖。
錐狀分布(Cone-Shape Distribution)
- 當Cohen's class分佈中的,且時,
- 其中,Cohen's class分佈會成錐狀分布。
- 右圖為不同的值下的錐狀分佈時頻分析圖。
喬伊-威廉斯(Choi-Williams)
- 當Cohen's class分佈中的時,Cohen's class分佈會成喬伊-威廉斯分布。
- 右圖為不同的值下的錐狀分佈時頻分析圖。
科恩系列分佈優缺點
- 優點:
- 1.可選擇適當的遮罩函數來避免掉交叉項問題 。
- 2.具有高清晰度。
- 缺點
- 1. 需要較高的計算量與時間。
- 2. 缺乏良好的數學特性。
科恩系列分佈的實現
簡化方法一:不是所有的的值都要計算出
- 對或,若,則
簡化方法二:注意,這個參數和輸入及輸出都無關
- ,其中
- ,由於和輸入無關,可事先算出,因此可簡化成兩個積分式。
簡化方法三:使用摺積方法(convolution)
- ,其中
- 。對或是,則
- ,上式為一摺積式。
模糊函數 (Ambiguity Function)
模糊函數的定義為:
Modulation 和 Time Shifting 對模糊函數的影響
我們來看一下 對於模糊函數的影響
(1) 假設 是一個高斯函數: , 其中
那麼我們可以得到 , 代入模糊函數 中:
(2) 假設 是一個經過 shifting 和 modulation 的高斯函數:
那麼我們可以得到 , 代入模糊函數 中:
我們可以看到 ,
因此我們可以得出 time shifting 和 modulation 並不會影響
積分後,
所以 在 的地方會有最大的
交叉項 Cross-term 問題
上述所列出來的是當 只有一項而已 (one term only),如果 有兩項以上的元素構成 (more than two terms), ,依然會有交叉項 (cross-term) 的問題存在。
假設 , 其中
將 代入模糊函數 中:
- 其中
Auto - terms
Cross - terms
(1)
(2)
因此,我們目前得到 (auto-terms) 和 (cross-terms) 的公式,我們再仔細的分析 auto-terms 和 cross-terms 分別發生最大值的位置。

首先,先看 Auto-terms:
- 最大值發生在 的地方
- 最大值發生在 的地方
而 Cross-terms:
- 最大值發生在 的地方
- 最大值發生在 的地方
換句話說,如果我們繪製一個 x軸為 , y軸為 的座標圖,Auto-terms發生在原點 的位置,而 Cross-terms 則是以原點為對稱中心,在第一象限和第三象限的位置,
這也是為什麼可以透過一個低通函數來濾除雜訊,把主成分 Auto-terms 分離出來,避免交叉項的問題。
與 維格納分布 Wigner Distribution Function 的不同
維格納分布是由尤金·維格納於 1932 年提出的新的時頻分析方法,對於非穩態的訊號有不錯的表現。
相較於傅立葉轉換或是短時距傅立葉轉換,維格納分布能有比較好的解析能力。
維格納分布的定義為:
如果我們假設 是一個具有弦波特性的訊號,
那麼將此 代入維格納分布中,
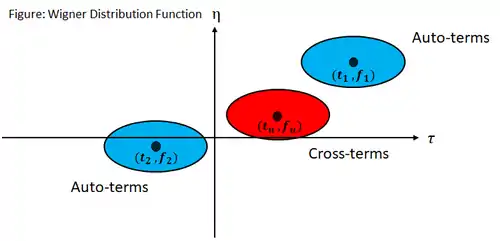
所以當 時, 在 的地方會有最大值。
換句話說,當 有 modulation 或是有 time shifting 的情況發生時,會影響維格納分布 (Wigner Distribution Function) 最大值 的位置
然而,對於科恩系列分布 (Cohen's class distribution)而言,time shifting 和 modulation 並不會影響
參考
- Jian-Jiun Ding, Time frequency analysis and wavelet transform class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2007.
- Jian-Jiun Ding, Time frequency analysis and wavelet transform class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2018.