穆迪圖

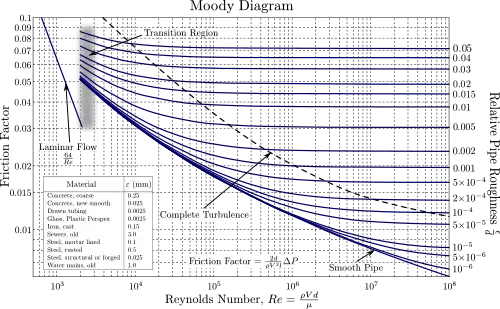
穆迪圖，其橫軸和縱軸分別是雷諾數及達西摩擦因子，其中有多條曲線，對應不同相對粗糙度（標示在右側）下的關係

穆迪圖標示了在流體不同雷諾數、不同流動形態（層流或紊流）及不同相對粗糙度下的達西摩擦因子，其中相對粗糙度是以表面粗糙度的平均高度和管路直徑的比值${\displaystyle \epsilon \over d}$。

穆迪圖可用來計算管路中的壓降${\displaystyle \Delta P}$，單位為Pa（或是水頭損失${\displaystyle h_{\mathrm {f} }}$，單位為公尺）或是流率。水頭損失（head loss）可以用達西–威斯巴哈方程式計算：

${\displaystyle {h_{\mathrm {f} }=f{\frac {l}{d}}{\frac {V^{2}}{2\,g}}};}$

而用下式可以計算壓降：

${\displaystyle \Delta P=\rho \,g\,h_{\mathrm {f} }}$或其直接表示為${\displaystyle \Delta P=f{\frac {\rho V^{2}}{2}}{\frac {l}{d}},}$

其中

${\displaystyle \rho }$為流體密度

${\displaystyle V}$為管路中平均速度

${\displaystyle f}$為由穆迪圖中求得的達西摩擦因子

${\displaystyle l}$為管路長度

${\displaystyle d}$為管路直徑

穆迪圖可分為層流及紊流二種流動形態。層流時達西摩擦因子的解析解由法國科學家讓·路易·馬利·普瓦澤伊所求得，為${\displaystyle {\frac {64}{Re}}}$，此區域中相對粗糙度對摩擦因子沒有顯著影響。紊流時達西摩擦因子及雷諾數的關係較複雜，可以用包括摩擦因子${\displaystyle f}$的科爾布魯克方程（Colebrook equation）來描述：

${\displaystyle {1 \over {\sqrt {\mathit {f}}}}=-2.0\log _{10}\left({\frac {\frac {\epsilon }{d}}{3.7}}+{\frac {2.51}{Re{\sqrt {\mathit {f}}}}}\right).}$

1944年時路易斯·費理·穆迪繪製達西摩擦因子和雷諾數及相對粗糙度的之間的關係，即為今天所見的穆迪圖[1]。

摩擦因子除了達西摩擦因子外，還有一個是范寧摩擦因子，其數值是達西摩擦因子的四分之一。達西摩擦因子較常用在土木工程及機械工程的領域中，而范寧摩擦因子較常用在化學工程的領域中。

可以用下式由范寧摩擦因子計算水頭損失：

${\displaystyle {h_{\mathrm {f} }=4f{\frac {l}{d}}{\frac {V^{2}}{2\,g}}},}$

也有對應范寧摩擦因子的穆迪圖，其特點是層流區的解析解為${\displaystyle {\frac {16}{Re}}}$。

• 達西摩擦因子公式