立方和
立方和是數學公式的一種,它屬於因式分解、乘法公式及恆等式,被普遍使用。立方和是指一個立方數,加上另一個立方數,即是它們的總和。公式如下:[1]
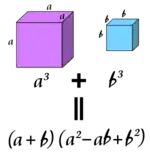
立方和的簡單圖解
立方和被因式分解後,答案分別包含二項式及三項式,與立方差相同。
驗證
主驗證
驗證此公式,可透過因式分解,首先設以下公式:
然後代入:
透過因式分解,可得:
這樣便可驗證:
幾何驗證

圖象化
透過繪立體的圖像,也可驗證立方和。[2] 根據右圖,設兩個立方,總和為:
把兩個立方體對角貼在一起,根據虛線,可間接得到:
要得到,可使用的空白位置。該空白位置可分割為3個部分:
把三個部分加在一起,便得:
之後,把減去它,便得: 上公式發現兩個數項皆有一個公因子,把它抽出,並得:
可透過和平方公式,得到:
這樣便可證明
反驗證
透過也可反驗證立方和。
以上計算方法亦可簡化為一個表格:
| x) | |||
|---|---|---|---|
這樣便可證明
立方差
立方差也可以使用立方和來驗證,例如:
把兩個數項都轉為立方數:
運用負正得負,可得:
然後運用立方和,可得:
這個方法更可驗證到立方差的公式是
兩組立方和的數
有些整數可以有兩個立方和組合,[3] 而最少的,已是過千的1729。它是兩組不同的立方和:
下一個同樣有兩個立方和組合的整數是4104:
首十個兩組立方和的數:1729、4104、13832、20683、32832、39312、40033、46683、64232、65728
參考文獻
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.