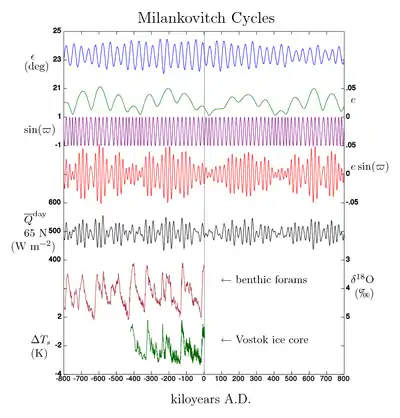
米蘭科維奇循環
米蘭科維奇循環(Milankovitch cycles)是塞爾維亞的地球物理学家兼天文學家米盧廷·米蘭科維奇的气候变化理论。米蘭科維奇计算了过去数百万年地球的離心率、轉軸傾角和軌道的進動的变化,发现了这些参数与地球上氣候模式,尤其是冰川期的关系。
地球軌道傾角的大約每26,000年完成繞行一周的完整進動週期。在這同時,橢圓軌道旋轉也以緩慢的21,000年引導著季節和軌道之間的變化。另一方面,地球的自轉軸和軌道平面之間的傾角以41,000年的周期在22.1度到24.5度之間搖擺著,現在的角度是23.44度,並且還在減少中。此運動稱為章动。
其它還有約瑟夫·阿德馬、詹姆士·克洛爾和其他人提出先進的天文理論,但是仍有所疑慮,由於要和過去的時間完全確切結合是很重要的證據,因此很難得到驗證。直到深海岩蕊和詹姆士·海斯、約翰·英柏瑞和尼可拉斯·沙克頓的沉積層報告:《地球軌道的變動:冰河期的定標》,發表在1976年的《科學》期刊[1],理論才呈現目前的狀態。
地球的變動
地球围绕自轉軸自转和在軌道上繞著太陽公转的过程中,会有幾個準週期的變化發生。运动曲線上虽然有大量的正弦成分,但仅有幾個成分在主導[2]。米蘭科維奇研究軌道離心率、傾角、和進動的變化。這些在運動和方向上的變化改變了太陽輻射抵達地球的方向和數量,這是所知的太陽強迫作用(一個輻射強迫作用的例子)。北極附近地區由於有大量的陸地,變動被認為比較重要,這是因為陸地的反應比海洋快速。
軌道形狀(離心率)


地球的軌道是橢圓形,而離心率是測量橢圓與圓形的偏差。地球軌道的形狀在接近圓形(低離心率的0.005)到輕度的橢圓(高離心率的0.058)之間變化,平均的離心率是0.028,此變化的主要週期是413,000年(離心率改變±0.012)。其它較主要的週期是是95,000年和125,000年(聯結的週期是400,000年),而分異鬆散的週期是100,000年)。目前的離心率是0.0167。
如果地球是唯一環繞著太陽的行星,它的離心率即使經過數百萬年也不會有感覺得到的輕微變化,地球軌道離心率的改變主要是受到木星和土星不同引力的交互作用影響。橢圓軌道的離心率雖然會改變,但橢圓軌道的半長軸不會改變。從攝動理論的觀點,使用天體力學計算軌道的演化,半長軸是絕熱不變量。依據克卜勒第三定律,軌道週期是由軌道半長軸測定的。因此,地球的軌道週期,恆星年,當軌道逐漸變化時,長度也仍然保持著不變。當半短軸隨著離心率的增加縮短時,季節的變化會加劇[3],但根据克卜勒第二定律,行星的平均太陽輻射變化在低離心率時只有微量的變化。
同樣的平均輻射與平均溫度並不會有相對應的關聯性(由於史蒂芬-波茲曼定律是非線性的)。一個與溫度20°相對應的輻射,可以有±50 %的對稱變化(例如,來自季節的變化[4])。我們觀測到的溫度變化對應於平均16℃(也就是說偏差有n-4℃)。並且在一天之中的輻射變化(仍然對應於平均溫度20℃),我們觀察到的平均溫度是(對零熱容量)-113℃。
在最靠近太陽時(近日點)相對增加的太陽輻射大約是在距離太陽最遠時離心率的4倍。以目前的軌道離心率,這相當於增加6.8%入射的太陽輻射,而目前近日點和遠日點的差異只有3.4%(510萬公里)。現在通過近日點的日期大約在每年的1月3日,而經過遠日點的日期大約是7月4日。當地球軌道最橢圓時,在近日點的太陽輻射量將比遠日點時大23%。
| 季節(北半球)持續時間 | |||
| 日期來源:美國海軍天文台 (页面存档备份,存于) | |||
| 年 | 日期:GMT | 季節持續時間 | |
|---|---|---|---|
| 2005 | 冬至 | 2005年12月21日18:35 | 88.99 days |
| 2006 | 春分 | 2006年3月20日18:26 | 92.75 days |
| 2006 | 夏至 | 2006年6月21日12:26 | 93.65 days |
| 2006 | 秋分 | 2006年9月23日4:03 | 89.85 days |
| 2006 | 冬至 | 2006年12月22日0:22 | 88.99 days |
| 2007 | 春分 | 2007年3月21日0:07 | 92.75 days |
| 2007 | 夏至 | 2007年6月21日18:06 | 93.66 days |
| 2007 | 秋分 | 2007年9月23日9:51 | 89.85 days |
| 2007 | 冬至 | 2007年12月22日06:08 | |
軌道力學要求季節的長度與季節的象限領域成正比,因此在離心率的極端值時,在軌道遠心點端的季節持續的時間也會大幅的增長。當秋天和冬天是在出現在近心端時,如同目前北半球的狀態,地球在軌道上的移動速度是最快的,因此秋天和冬天會比春天和夏天稍短一些。像這樣,夏天比冬天長4.66天,春天比秋天長2.9天。
轉軸傾角(傾角/黃道赤道交角)

地球的轉軸傾角(傾斜)是地球的轉軸相對於軌道平面的角度。角度變化的範圍是2.4°,在大約41,000年的週期內從傾斜22.1°緩慢的變化至24.5°並且再復原。當傾角增加時,日照(進入的太陽輻射)在季節週期上的振幅也增加;在兩個半球的夏季都會接收到更多的太陽輻射通量,而冬季的輻射通量減少。但是,这种冬夏两季的反相变化在地表各处幅度不尽相同。當傾角增加時,高緯度的全年日照量會增加,而低緯度接收的全年日照量會減少。
現在地軸傾角處在逐漸變小的趨勢,使四季變化較和緩(暖冬及涼夏),因此有氣候冷卻的傾向。地球上大部分的冰雪位在高緯度,傾角減小時,兩個半球在夏季接收更少的日照量,並且高緯度地區的日照量亦縮減,涼爽的夏天造成先前在冬天的冰雪融化量減少,促使冰河期的開始。但是,沒有氣候變化與軸傾角極端值變化之間有意義的關聯。
科學家利用電腦模型研究更極端的地軸傾斜,比那些實際發生過更高的軸傾角,引發高緯度的極端氣候,以個別的研究能否威脅目前已經存在地球上的高等生物型態的生命。它們注意到高傾角並不能完全的消除一顆行星的生物,但會使它更難以茁狀和成長,而且也會讓現今存在於土地上的溫血生物衰弱.[5]。
目前地球相對於軌道平面的傾角是23.44度,大約是在各個極端值的中間。傾角是在週期的減少階段中,大約西元10,000年會達到其最小值。這一趨勢的本身往往會造成溫暖的冬季和涼爽的夏季,但是增強的溫室氣體可能會超越這種變化的影響。
軸向進動
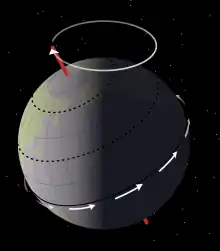
地球自轉軸的方向相對於恆星的變化稱為進動,週期大約是26,000年。這種陀螺的運動是由於太陽和月球對固體的地球,加上地球的形狀是扁橢球而不是理想的球,所施加的潮汐力,而太陽和月球有著大約一致的效果。
當自轉軸的方向在軌道的近日點朝向太陽時,一個極半球的季節有著較大的變化而另一個極半球的季節變化較為溫和。在近日點時是夏季的半球,接收到的太陽輻射會相對應的增加,而這個半球在冬季也會相對的較為寒冷。另一個半球則會有較溫暖的冬季和較為涼爽的夏季。
當地球的近日點和遠日點是朝向分點時,北半球和南半球有著相似的季節分布狀態。
在目前,當南半球的夏季時地球位於近日點,並且在遠日點時是南半球的冬季。因此,當其它的因素都相同時,南半球的季節會比北半球的較為極端。
拱線進動
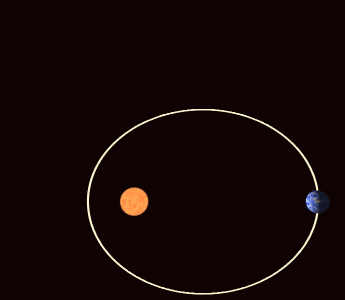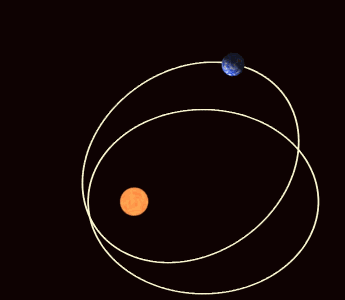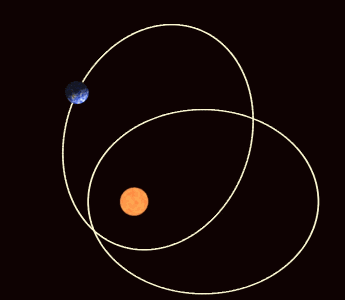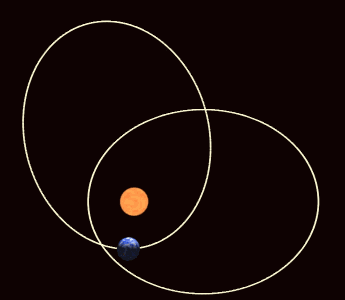
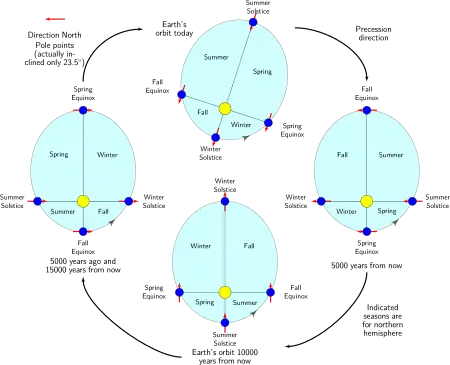
另一方面,橢圓軌道本身在空間中的行進,主要是受到木星和土星交互作用的結果。這種軌道進動和陀螺旋轉軸的運動是有著相同的意義,會使分點歲差相對於近日點進動的週期從25,771.5年縮短至大約為21,636年。
軌道傾角
地球軌道的傾角會在現在的軌道平面上以70,000年的週期向上和向下漂移。米蘭科維奇沒有研究這種三維空間的運動,這種運動被稱為黃道進動或是行星進動。
近期的研究人員注意到這種軌道的漂移也會相對於其他的行星軌道移動。不變平面,代表太陽系角動量的平面,大約就是木星的軌道平面。地球的軌道以100,000年的周期相對於不變的平面傾斜;很偶然的機會,這非常類似於100,000年的離心率週期。這個100,000年的週期與100,000年的冰河期週期模式相符合。
不變的平面中曾被認有塵埃和其它碎片形成的盤面,並且會通過幾種可能的手段影響到地球的氣候。地球目前在每年的1月9日和7月9日通過不變平面,雷達的偵測顯示這時流星和相關的夜光雲的數量都有增加 [6][7]。
使用南極冰核中困住的氣泡中氣體的氫氮比率進行的年代學研究,這似乎可以直接反應當地的日照,從冰核中記錄的氣候對應出北半球日照的結論,一如米蘭科維奇的假說(Kawamura et al., Nature, 23 August 2007, vol 448, p912-917)。這是驗證米蘭科維奇假說追加的一個新方法,並且與100,000年週期的"傾斜"理論是不吻合的。
問題
因為觀測到的氣候週期正好符合了軌道週期,使軌道理論獲得了壓倒性的支持。然而,在理論的滿足和觀測上還是有幾個困難。

十萬年的問題
100000年的問題是,按照理論,離心率的變化,相比於與太陽強迫有關的轉軸傾角變化或軸向進動變化,對氣候的影響較小。但是同位素分析表明,氣候變化的主導週期為約10萬多年。
参考文献
引用
- Hays, J.D.; Imbrie, J.; Shackleton, N.J. . Science. 1976, 194 (4270): 1121–1132. PMID 17790893. doi:10.1126/science.194.4270.1121.
- Girkin, Amy Negich. (PDF) (Master of Science论文). Miami University. 2005 [2010-10-08]. (原始内容 (PDF)存档于2014-01-06).
- Berger A., Loutre M.F., Mélice J.L. (PDF). Clim. Past Discuss. 2006, 2: 519–533 [2010-10-11]. doi:10.5194/cpd-2-519-2006. (原始内容 (PDF)存档于2013-05-12).
- (PDF).
|chapter=被忽略 (帮助); - Williams, D.M., Pollard, P. (PDF). Inter. J. Astrobio. 2002, 1: 21–9 [2010-10-11]. (原始内容 (PDF)存档于2013-08-22).
- Richard A Muller, Gordon J MacDonald. . Science. 1997, 277 (1997/07/11): 215–8. doi:10.1126/science.277.5323.215.
- . Richard A Muller. [March 2, 2005]. (原始内容存档于2018-07-10).
来源
- 王乾盈、王作台 等.《基礎地球科學》. 台北:全華圖書股份有限公司,1996年:p. 145. [2008年7月4日]. ISBN 978-957-21-5808-1.
- English Wikipedia,Milankovitch cycles (页面存档备份,存于),2008年6月30日
延伸讀物
- Roe G. . Geophysical Research Letters. 2006, 33: L24703. doi:10.1029/2006GL027817. This shows that Milankovitch theory fits the data extremely well, over the past million years, provided that we consider derivatives.
- Zachos J, Pagani M, Sloan L, Thomas E, Billups K. . Science. 2001, 292 (5517): 686–693. PMID 11326091. doi:10.1126/science.1059412.
This review article discusses cycles and large-scale changes in the global climate during the Cenozoic Era.
外部連結
| 维基共享资源中相关的多媒体资源:Milankovitch cycles |
- Milankovitch Cycles and Glaciation
- The Milankovitch band
- Some history of the adoption of the Milankovitch hypothesis (and an alternative) (页面存档备份,存于)
- More detail on orbital obliquity also matching climate patterns (页面存档备份,存于)
- Graph of variation in insolation (页面存档备份,存于) Note 20,000 year, 100,000 year, and 400,000 year cycles are clearly visible.
- . On the Shoulders of Giants. [January 15, 2010]. (原始内容存档于2016-03-03).
- Potential Problems with Milankovitch Theory (页面存档备份,存于) by Sean Pitman (页面存档备份,存于)
- The Seasons (页面存档备份,存于)
- The NOAA page on Climate Forcing Data (页面存档备份,存于) includes (calculated) data on orbital variations over the last 50 million years and for the coming 20 million years.
- The orbital simulations by Varadi, Ghil and Runnegar (2003) provide another, slightly different series for orbital eccentricity, and also a series for orbital inclination
- ABC: Earth wobbles linked to extinctions (页面存档备份,存于)