结构光三维扫描仪

基于双相机的条纹结构光图案示意图（双相机可以避免遮挡）

比较知名的制作条纹图案的方法有两种：激光干涉法和投影法。

激光干涉法基于两个宽的平面激光束前端。它们的干涉可以产生规则等距的线图案。通过改变这些光束之间的角度可以获得不同的图案尺寸。该方法易于精确的生成具有无限景深的精细图案。缺点是成本高，难以提供理想的光束几何形状以及典型的激光效果，例如斑点噪声以及部分光束从物体的反射带来的自干扰。通常无法调制独特的条纹，比如格雷码。

投影法使用不相干的光，并且基本上像视频投影仪一样工作。 使光线通过数字化的空间光调制器来生成图案，通常基于三种当前最广泛使用的数字投影技术之一：透射液晶，硅上反射液晶（LCOS）或数字光处理（DLP；移动微镜）调制器，各有优劣势。同时也存在其他投影方法。

由于显示器中的像素边界，数字显示投影仪产生的图案具有较小的不连续性，但由于轻微的散焦使边界差异变得比较均匀，从而可以忽略这种不连续性。

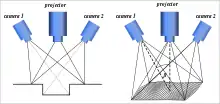
典型的测量组件由一台投影仪和至少一台摄像机组成，在很多应用中，在投影器两侧各安装一个相机是比较常见的结构设计。

不可见（或无法察觉）的结构化灯光使用时不会干扰其他计算机视觉任务的结构化灯光，而不可见的投影图案会让使用者对其原理感到比较困惑。比如使用红外光或具有极高帧频的两个正好相反的图案交替使用。[2]

在实验室的一台三维扫描仪。标定板在桌面右侧位置。

必须通过使用特殊的校准图案和表面对测量设备进行校准，以补偿光学器件和视角造成的几何变形。数学模型用于描述投影仪和照相机的成像特性。从本质上讲，该模型基于針孔相機的简单几何特性，还必须考虑到投影仪和相机镜头的几何畸变和光学像差。相机的参数及其在空间中的位置姿态可以使用摄影测量光束法平差通过一系列校准测量来确定。

在观察到的条纹图案中包含若干深度信息。任何单个条纹的位移都可以直接转换为3D坐标。因此必须识别单个条带。例如可以通过跟踪或计数条带（图案识别方法）来实现。另一种常见的方法是投影交替的条纹图案，从而产生二进制格雷码序列，该序列标识出击中对象的每个单独条纹的数量。重要的深度信息也来自沿着物体表面的不同条纹宽度。条纹宽度是表面部分的陡度的函数，即高程的一阶导数。条带频率和相位提供类似的深度信息，并且可以通过傅里叶变换进行分析。 基于同样的目的近些年也在研究小波变换。

在很多实际应用中，采用将模式识别，格雷码和傅里叶变换相结合的一系列测量手段，来实现三维形状的完整且准确的重构。

另一种利用照相机景深的方法也属于条纹投影区域。[3]

也可以将投影图案用作结构插入场景中，以进行摄影测量。

条纹投影方法的光学分辨率取决于所用条纹的宽度及其光学质量。它也受光波长的限制。

由于景深，相机分辨率和显示分辨率的限制，条纹宽度的无限制减小没有太大意义。 因此，相移方法被广泛使用：用稍微偏移的条纹进行至少3次曝光，通常约10次曝光。 该方法的第一个理论推论依赖于具有正弦波形强度调制的条纹，但是该方法也适用于“矩形”调制条纹，如LCD或DLP显示器所提供的。通过相移，可以达到1/10条纹间距级别的细节。

因此，当前的光学条纹图案轮廓测定法可以实现低至光波长的细节分辨率，实践中小于1微米，对于较大的条纹图案，则可以达到大约条纹宽度的1/10。 对图像的几个像素进行插值可以产生可靠的高程分辨率，并且精度低至1/50像素。

可以使用大条纹图案来测量大尺寸对象。 实际应用中有测量几米到几十米的物体的实践。

典型的精度数字为：

• 2英尺（0.61m）宽的平面度，可以到10微米（0.00039英寸）。
• 马达燃烧室的形状达到2微米（7.9×10-5英寸）（高程），容积精度比容积计量好10倍。
• 2英寸（51毫米）大的物体，约1微米（3.9×10-5英寸）
• 叶片边缘的半径例如10微米（0.00039英寸），精度到±0.4 μm

由于该方法一次只能从一个角度测量形状，因此必须从不同角度的不同测量中组合完整的3D形状。这可以通过在对象表面粘贴定位标志点并随后通过匹配这些标志点来组合各个视角的数据来实现。通过将物体安装在电动转盘或CNC定位设备上，该过程可以自动化。标志点也可以应用在定位设备上，而不是对象本身。

收集的3D数据可用于恢复CAD数据（计算机辅助设计）、逆向工程；手工作品或雕塑、自然物体或人工制品的三维建模。

与所有光学方法一样，反射或透明表面难度较大。反射会导致光线原理相机或直接反射到其光学元件中。在这两种情况下，都可以超出摄像机的动态范围。透明或半透明的表面也会造成很大的困难。在这些情况下，仅出于测量目的，用薄的不透明清漆涂覆表面是一种常见的做法。一种最新方法是通过在光源（例如，投影仪）和要扫描的对象之间插入一维漫射器来处理高反射和镜面反射的对象。[4] 有的学者已经提出了替代性的光学技术来处理完全透明和镜面物体。[5]

两次反射和相互反射会导致条纹图案被多余的光线覆盖，从而难以被准确的检测识别。 因此，高反射的腔体和凹形物体很难处理。 由于次表面散射现象，也难以处理诸如皮肤，大理石，蜡，植物和人体组织之类的半透明材料。 最近，计算机视觉界已经在努力通过重新设计照明模式来处理这种光学上复杂的场景。[6] 这些方法已显示出对传统困难物体（例如高镜面金属凹度和半透明蜡烛）的3D扫描结果的希望。[7]

尽管在大多数结构光方法中必须为每张图片拍摄几种模式，但是高速结构光扫描可用于许多应用程序，例如：

• 在生产过程中对零件进行在线精密检查。
• 卫生保健应用，例如实时测量人体形状或人体皮肤的微观结构。

基于运动图像的应用也有被开发，例如用于三维电视的空间场景数据的获取。