置换检验
置换检验()是统计学上一种基于反证法、重抽样原则的非参数性检验,由罗纳德·艾尔默·费希尔()与E・J・G・皮特曼()于20世纪30年代最早提出[1]。
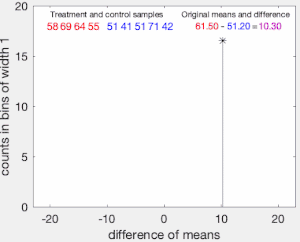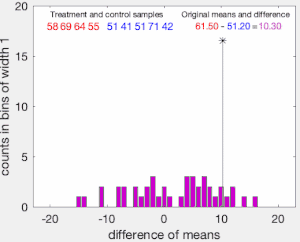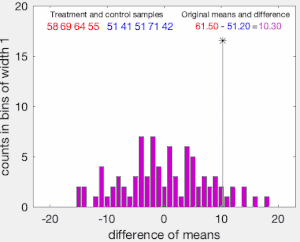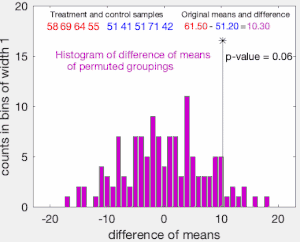
置换检验的零假设(虚无假设)为,即所有样本都服从同一分布。置换检验通过对比样本置换后的检验统计量与置换前的检验统计量来决定是否拒绝零假设、接受备择假设。
方法
进行置换检验前,首先计算两样本(样本容量设为、)之间原本的检验统计量。检验统计量可以是两样本间平均数之差、方差之差,或t值、卡方检验中的值等,但这一统计量原则上在重新抽样后应大致符合某一统计学分布(如正态分布、t分布、f分布等)[2]:355-360。随后,将两个样本打乱后再重新选出两组容量等于之前两样本的新样本(即两个样本容量同样为、的样本)并计算新的检验统计量。如接受零假设,即样本源于同一分布,则随机抽样计算出的新检验统计量应不难大于最初置换前算出的两样本间检验统计量(如为双侧检验,则是其绝对值应不难大于置换前算出的两样本间检验统计量),即这个概率应大于设定的I型错误(假阳性)概率。反之,则拒绝零假设,接受备择假设,即样本来自不同的分布。实际计算时,当两个样本容量都很大时,穷举所有置换并计算新的检验统计量所需的计算量过于庞大,因此常采用蒙特卡罗模拟的办法进行置换检验。蒙特卡罗模拟中,只做一定次数的打乱重选(置换)并计算检验统计量,再用这些计算出的检验统计量与置换前原本的检验统计量进行对比[3][4]。
优势与不足
置换检验能用于两个分布不明且都不符合正态分布的样本之间的统计检验,是对较常用的t检验、方差分析(ANOVA)等参数检验的一个补充[5]。即使实验是非均衡设计(即样本容量不同),依然能够对样本进行置换检验[6]。
另一方面,和其他基于秩的非参数检验相似,置换检验是一种相对保守的检验。如果对两个差别较小的小样本进行置换检验,则很容易接受零假设、拒绝备择假设(即检验功效相对较低)[7][8]。
参见
- 非参数检验
- 置换方差分析
参考文献
- Boik, Robert J. . British Journal of Mathematical and Statistical Psychology (Wiley). 1987, 40 (1): 26–42. ISSN 0007-1102. doi:10.1111/j.2044-8317.1987.tb00865.x.
- Robert V. Hogg; Elliot A. Tanis; Dale L. Zimmereman. Ninth Edition (International). Pearson. 2015. ISBN 978-1-292-06235-8.
- . Oklahoma State University. Ordination Methods for Ecologists. [2022-12-04]. (原始内容存档于2023-06-08).
- Wilcox, Rand R. . . Elsevier. 2003: 237–284. doi:10.1016/b978-012751541-0/50029-8.
- Collingridge, Dave S. . Journal of Mixed Methods Research. 11 September 2012, 7 (1): 81–97. S2CID 124618343. doi:10.1177/1558689812454457.
- (PDF). Journal of Modern Applied Statistical Methods. Fall 2011, 1 (2): 202–522. (原始内容 (PDF)存档于May 5, 2003).
- Allison, D.B.; Page, G.P.; Beasley, T.M.; Edwards, J.W. . Chapman & Hall/CRC Biostatistics Series. CRC Press. 2005: 261 [2022-12-07]. ISBN 978-1-4200-2879-9. (原始内容存档于2022-12-07).
- Berger, Vance W. . Statistics in Medicine (Wiley). 2000-05-30, 19 (10): 1319–1328. ISSN 0277-6715. doi:10.1002/(sici)1097-0258(20000530)19:10<1319::aid-sim490>3.0.co;2-0.