肖克利-奎伊瑟极限

在物理学中，肖克利-奎伊瑟极限（亦称细致平衡极限、精细平衡转换效率极限或SQ极限，或物理学名词辐射效率极限）太阳能电池使用单PN结从电池中收集能量的理论最大效率，其中唯一的损失机制是太阳能电池中的辐射复合。它是由威廉·肖克利和Hans-Joachim Queisser于1961年在肖克利半导体实验室首次计算出来的，结果是1.1 eV时最高效率为30%[1]。此极限是利用光伏电池生产太阳能最基本的原理之一，并被认为是该领域最重要的贡献之一[2]。

光电转换效率的肖克利-奎伊瑟极限（不考虑太阳辐射）。曲线起波是由于大气层中的吸收带。在原始论文中[1]，太阳光谱由一个平滑曲线近似（6000K黑体光谱），所以效率光谱是平滑的，其值有微小差异。

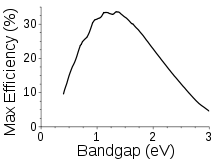
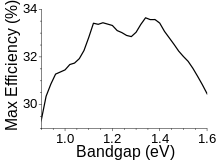
最初的计算使用6000K黑体光谱作为太阳光谱的近似值，随后的计算使用了测量的全球太阳光谱AM 1.5，并包括一个背面反射镜，它将带隙为1.34 eV的单结太阳能电池的最大太阳转换效率提高到33.16%[3]，也就是说，所有落在理想太阳能电池上的阳光（约1000 W/²）的能量中，只有33.7%能够转化为电能(337 W/²)。最流行的太阳能电池材料硅的带隙为1.1 eV，效率最高可达32%左右。现代商用单晶太阳能电池的转换效率约为24%，这种损耗很大程度上是由于实际需要，比如电池正面的反射和电池表面细线的光阻塞。

肖克利-奎伊瑟极限仅适用于单PN结的传统太阳能电池，多层太阳能电池可以（而且确实）超越这一极限，太阳能热和某些其他太阳能系统也可以。在极端极限下，对于具有无限层数的多结太阳能电池，正常日照时的极限为68.7%[4]，聚光日照时的极限为86.8%[5]（参见光电转换效率）。