自然對數
自然对数(英語:)為以数学常数e為底數的对数函数,標記作或,其反函数為指數函數。[註 1]
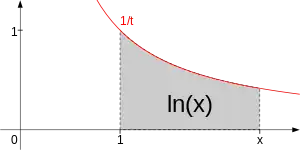
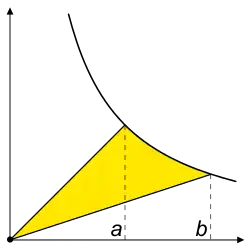
自然对数积分定義為對任何正實數,由 到 所圍成, 曲線下的面積 。如果小於1,則計算面積為負數。
則定義為唯一的實數 使得 。
歷史
十七世纪
約翰·納皮爾在1614年[3]以及约斯特·比尔吉在6年後[4],分別發表了獨立編制的對數表,當時通過對接近1的底數的大量乘冪運算,來找到指定範圍和精度的對數和所對應的真數。當時還沒出現有理數冪的概念,按後世的觀點,約翰·納皮爾的底數0.999999910000000相當接近[5],而约斯特·比尔吉的底數1.000110000相當接近自然對數的底數。實際上不需要做開高次方這種艱難運算,約翰·納皮爾用了20年時間進行相當於數百萬次乘法的計算,亨利·布里格斯建議納皮爾改用10為底數未果,他用自己的方法[6]於1624年部份完成了常用對數表的編制。
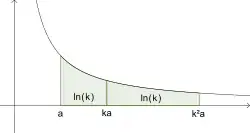
形如的曲線都有一個代數反導數,除了特殊情況對應於雙曲線的弓形面積,即雙曲線扇形;其他情況都由1635年發表的卡瓦列里弓形面積公式給出[7],其中拋物線的弓形面積由公元前3世紀的阿基米德完成(拋物線的弓形面積),雙曲線的弓形面積需要發明一個新函數。1647年圣文森特的格列高利將對數聯繫於雙曲線的弓形面積,他發現x軸上兩點對應的雙曲線線段與原點圍成的雙曲線扇形同對應的扇形,在時面積相同,這指出了雙曲線從到的積分滿足[8]:
1649年,萨拉萨的阿尔丰斯·安东尼奥將雙曲線下的面積解釋為對數。大約1665年,伊薩克·牛頓推廣了二項式定理,他將展開並逐項積分,得到了自然對數的無窮級數。“自然對數”最早描述見於尼古拉斯·麥卡托在1668年出版的著作《Logarithmotechnia》中[9],他也獨立發現了同樣的級數,即自然對數的麥卡托級數。
形式定義
歐拉定義自然對數為序列的極限:
正式定義為積分,
這個函數為對數是因滿足對數的基本性質:
這可以通過將定義了的積分拆分為兩部份,並在第二部份中進行換元來證實:
冪公式可如下推出:
第二個等式使用了換元。
自然對數還有在某些情況下更有用的另一個積分表示:
導數
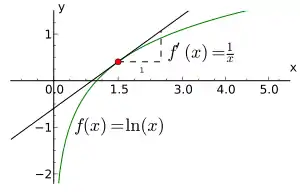
自然對數的導數為
證明一 (微積分第一基本定理):
设
设
用自然對數定義的更一般的對數函數,,根據其逆函數即一般指數函數的性質,它的導數為[13][14]:
根據鏈式法則,以為參數的自然對數的導數為
冪級數
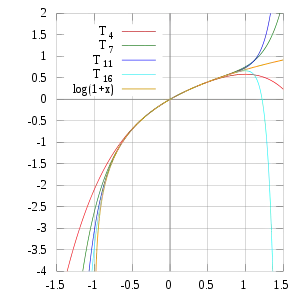
自然對數的導數性質導致了在0處的泰勒級數,也叫做麥卡托級數:
-
- 對於所有 但不包括
把代入中,可得到自身的級數。通過在麥卡托級數上使用歐拉變換,可以得到對絕對值大於1的任何有效的如下級數:
這個級數類似於贝利-波尔温-普劳夫公式。
還要注意到是自身的逆函數,所以要生成特定數的自然對數,簡單把代入中。
-
- 對於
自然數的倒數的總和
叫做調和級數。它與自然對數有密切聯繫:當趨於無窮的時候,差
與雙曲函數的關係
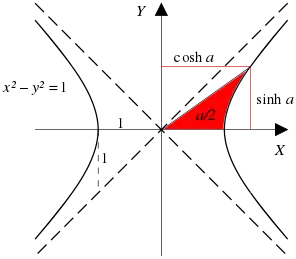
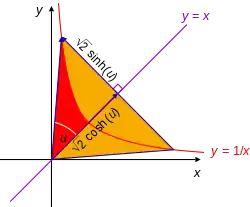
在18世紀,約翰·海因里希·蘭伯特介入雙曲函數[17],並計算雙曲幾何中雙曲三角形的面積[18]。對數函數是在直角雙曲線下定義的,可構造雙曲線直角三角形,底邊在線上,一個頂點是原點,另一個頂點在雙曲線。這裡以自然對數即雙曲角作為參數的函數,是自然對數的逆函數指數函數,即要形成指定雙曲角,在漸近線即x或y軸上需要有的或的值。顯見這裡的底邊是,垂線是。
通過旋轉和縮小線性變換,得到單位雙曲線下的情況,有:
單位雙曲線中雙曲線扇形的面積是對應直角雙曲線下雙曲角的。
連分數
儘管自然對數沒有簡單的連分數,但有一些廣義連分數如:
這些連分數特別是最後一個對接近1的值快速收斂。但是,更大的數的自然對數,可以輕易的用這些更小的數的自然對數的加法來計算,帶有類似的快速收斂。
例如,因為,2的自然對數可以計算為:
進而,因為,10的自然對數可以計算為:
複數對數
指數函數可以擴展為對任何複數得出複數值為的函數,只需要簡單使用為複數的無窮級數;這個指數函數的逆函數形成複數對數,並帶有正常的對數的多數性質。但是它涉及到了兩個困難: 不存在使得;並且有著。因為乘法性質仍適用於複數指數函數,,對於所有複數和整數。
所以對數不能定義在整個複平面上,並且它是多值函數,就是說任何複數對數都可以增加的任何整數倍而成為等價的對數。複數對數只能在切割平面上是單值函數。例如,或或等等;儘管,不能定義為或或,以此類推。
- 自然對數函數在複平面(主分支)上的繪圖
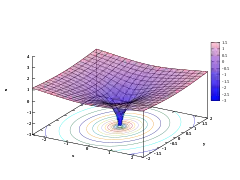 z = Re(ln(x+iy))
z = Re(ln(x+iy))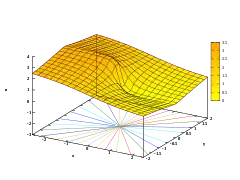
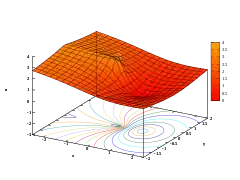
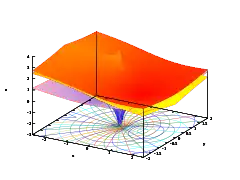 前三圖的疊加
前三圖的疊加
主值定義
對於每個非0複數,主值是虛部位於區間內的對數。表達式不做定義,因為沒有複數滿足。
要對給出一個公式,可以先將表達為極坐標形式,。給定,極坐標形式不是確切唯一的,因為有可能向增加的整數倍,所以為了保證唯一性而要求位於區間內;這個叫做幅角的主值,有時寫為或。則對數的主值可以定義為[19] :
例如,。
註釋
参考资料
- 例如哈代和賴特所著的《數論入門》"Introduction to the theory of numbers" (1.7, Sixth edition, Oxford 2008)的注解 "log x is, of course the 'Napierian' logarithm of x, to base e. 'Common' logarithms have no mathematical interest."(log x 當然是以e為基,x的「納皮爾」對數。「常用」對數在數學上毫無重要。)
- 證明:從1到b積分1/x,增加三角形{(0, 0), (1, 0), (1, 1)},並減去三角形{(0, 0), (b, 0), (b, 1/b)}。
- Ernest William Hobson, , Cambridge: The University Press, 1914
- Boyer, Carl B., , , New York: John Wiley & Sons, 1991, ISBN 978-0-471-54397-8
- 選取接近e的底數b,對數表涉及的bx為單調增函數,定義域為0到1而值域為1到b;選取接近1/e的底數b,對數表涉及的bx為單調減函數,定義域為0到∞而值域為1到0。
- 以這個接近1的數為基礎。
-
博納文圖拉·卡瓦列里在1635年的《Geometria indivisibilibus continuorum nova quadam ratione promota》中給出定積分:
- 設a=1,x軸上[a,b]兩點對應的雙曲線線段與原點圍成的雙曲線扇形面積為f(b),[c,d]對應的扇形面積為f(d)-f(c),d=bc,即為f(bc)-f(c),當且僅當f(bc)=f(b)+f(c)時,兩雙曲線扇形面積相等。
- J. J. O'Connor; E. F. Robertson, , The MacTutor History of Mathematics archive, September 2001 [2009-02-02], (原始内容存档于2012-02-19)
-
卡瓦列里弓形面積公式,對於負數值的n(x的負數冪),由於在x = 0處有個奇點,因此定積分的下限為1,而不是0,即為:
- Maor, Eli, , Princeton University Press, 2009, ISBN 978-0-691-14134-3,sections 1, 1.
Eves, Howard Whitley, , The Saunders series 6th, Philadelphia: Saunders, 1992, ISBN 978-0-03-029558-4, section 9-3
Boyer, Carl B., , New York: John Wiley & Sons, 1991, ISBN 978-0-471-54397-8, p. 484, 489 -
在最初的概念下,底數是接近1的數,而對數是整數;經過簡單變換後,底數變大了,成為接近數學常量e的數,而對數變小了,成為 x/n。 - Lang 1997, section IV.2
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research. (原始内容存档于2011-07-18) (英语).
- Kline, Morris, , Dover books on mathematics, New York: Dover Publications, 1998, ISBN 978-0-486-40453-0, p. 386
- Havil, Julian, , Princeton University Press, 2003, ISBN 978-0-691-09983-5, sections 11.5 and 13.8
- Eves, Howard, , Courier Dover Publications: 59, 2012, ISBN 9780486132204,
We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions.
- Ratcliffe, John, , Graduate Texts in Mathematics 149, Springer: 99, 2006 [2014-03-28], ISBN 9780387331973, (原始内容存档于2014-01-12),
That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
- Sarason, Section IV.9.
延伸阅读
- John B. Conway, Functions of one complex variable, 2nd edition, Springer, 1978.
- Serge Lang, Complex analysis, 3rd edition, Springer-Verlag, 1993.
- Gino Moretti, Functions of a Complex Variable, Prentice-Hall, Inc., 1964.
- Donald Sarason, Complex function theory (页面存档备份,存于), 2nd edition, American Mathematical Society, 2007.
- E. T. Whittaker and G. N. Watson, A Course in Modern Analysis, fourth edition, Cambridge University Press, 1927.