蒙日圆
法國數學家加斯帕爾·蒙日發現:與橢圓相切的兩條垂直切線的交點的軌跡方程是。这一结论被称为蒙日圆。
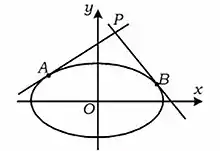
證明
設分別為橢圓的左右焦點,焦距為。設點分別為點關於,關於的對稱點。由橢圓的光學性質[lower-alpha 1]知,,及,,分別三點共線,由橢圓定義有。設交直線于點,交直線於點,分別延長,交於點,則,。在矩形中,由平面幾何知識易知,於是。
在雙曲線中的結論
與雙曲線相切的兩條垂直切線的交點的軌跡方程是。
在拋物線中的結論
與拋物線相切的兩條垂直切線的交點的軌跡方程是(可以看成是半徑無窮大的圓)。
註釋
- 经过椭圆上一点的法线,平分这一点的两条焦点半径的夹角。
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.