面 (幾何)

在立体几何中，立体几何体的邊界被称作面或表面[1][2]，更嚴謹地說，面是立体几何体的一個平坦表面[3]，而不平坦的面通常稱為曲面，而所有表面的總和稱為表面積[4]。在高维度几何以及高维的多胞形中，面也被用来指代构成多胞形的一个组成元素，通常會跟隨其維度一同稱呼，例如三維的元素稱為3-面。[5]

多边形面

在基础几何学中，面是指位於多面體邊界的多邊形[5]，換句話說即多面体是一个由多边形构成的三维几何体，构成多面体的这些多边形就被称为面[6]。 

例如：正方体有六个面，三棱锥有四个面。广义来说，面也可用来指代四多胞形的一个二维边界，就如我们说四维超正方体有24个正方形面。

面的例子
凸正多面體 星形正多面體 正鑲嵌圖 雙曲鑲嵌 四維z多胞體
{4,3} {5/2,5} {4,4} {4,5} {4,3,3}

立方體的每個頂點都是3個正方形面的公共頂點[7]
小星形十二面體的每個頂點都是5個五角星面的公共頂點[8]
正方形鑲嵌的每個頂點都是4個正方形面的公共頂點[9]
五階正方形鑲嵌的每個頂點都是5個正方形面的公共頂點[10]
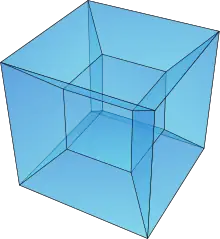超立方體的每條邊都是3個正方形面的公共稜[11]

多面体的面的数量

在三维空间中，任何凸多面体的欧拉示性数为2。欧拉示性数 可以通过以下公式计算：

[註 1]

以上式子中，V 是顶点的数量，E 是边的数量，F 是面的数量。例如，正方体有12条边，8个顶点和6个面。那么我们可以计算得正方体的欧拉示性数为2。

維面
条目：維面

在幾何學中，維面（Facet）又稱為超面（hyperface[12]）是指幾何形狀的組成元素中，比該幾何形狀所在維度少一個維度的元素[13]

多維面

在幾何學中，維面一詞前面若加一個整數，則代表一幾何結構中維度為該整數的元素，此概念不應與維面混淆。例如k維面代表幾何結構中維度為k的元素，又稱k面、k-面或k維元素而在更高維度中，有時會稱為k維胞，這一用法並未限定元素的所屬維度。[5][14][15]例如立方體的多維面包括了空多胞形（負一維面）、頂點（零維面）、邊（一維面）、正方形（二維面，一般稱面）和其本身（三維面，一般稱體）。正式地，對於一個多胞形P，多維面的定義是與一個「不與P內部相交的封閉半空間」的相交幾何結構（如交點、交線或交面等）[5][15]。多胞形中的多維面集合中同時也包含了多胞形本身和空多胞形。[14][15]

參見

註釋
  1. 这行式子应理解为： 的定义式是
  2. 在晶体学中有多个面的概念，如反映面是通过反映这一对称操作得到的，用符号P表示，如单斜晶系晶体反映面之数目为1。此外，还有滑移面的概念。
    晶体学中的另一个面的概念是晶体的晶面，可用h, k, l表示，其表示方法如{100}、{010}等。[16]

参考来源
  1. . 教育部重編國語辭典修訂本. [2019-09-16]. （原始内容存档于2020-04-09）.
  2. . 教育部重編國語辭典修訂本. [2019-09-16]. （原始内容存档于2020-04-09）.
  3. Eleventh. Springfield, MA: Merriam-Webster. 2004.
  4. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  5. Matoušek, Jiří, , Graduate Texts in Mathematics 212, Springer, 5.3 Faces of a Convex Polytope, p. 86, 2002 [2017-11-11], （原始内容存档于2019-06-10）.
  6. Cromwell, Peter R., , Cambridge University Press: 13, 1999 [2017-11-11], （原始内容存档于2019-06-13）
  7. Van Cleve, J. . Oxford University Press. 2003. ISBN 9780195347012. LCCN 98026825.
  8. Weber, Matthias. 220. 2005: 167–182. |journal=被忽略 (帮助) pdf （页面存档备份，存于）
  9. Tilings and Patterns, from list of 107 isohedral tilings, p.473-481
  10. . . Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
  11. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  12. N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.1 Polytopes and Honeycombs, p.225
  13. Matoušek (2002), p. 87; Grünbaum (2003), p. 27; Ziegler (1995), p. 17
  14. Grünbaum, Branko, , Graduate Texts in Mathematics 221 2nd, Springer: 17, 2003 [2019-09-16], （原始内容存档于2013-10-31）.
  15. Ziegler, Günter M., , Graduate Texts in Mathematics 152, Springer, Definition 2.1, p. 51, 1995 [2019-09-16], （原始内容存档于2019-06-12）.
  16. 钱逸泰. 结晶化学导论（第3版）. 合肥: 中国科学技术大学出版社, 2005. ISBN 7-312-01804-1/O·31
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.