轉移矩陣

随机矩阵描述了在一个有限状态空间 S 上的马尔可夫链 ${\displaystyle {\boldsymbol {X}}_{t}}$。

如果在一个时间步长内从 ${\displaystyle i}$ 到${\displaystyle j}$移动的概率为 ${\displaystyle \operatorname {Pr} (j|i)=P_{i,j}}$ ，随机矩阵 ${\displaystyle P}$ 的第 ${\displaystyle i}$ ，第 ${\displaystyle j}$ 元素由 ${\displaystyle P_{i,j}}$ 给出，例如，

${\displaystyle P=\left[{\begin{matrix}P_{1,1}&P_{1,2}&\dots &P_{1,j}&\dots &P_{1,S}\\P_{2,1}&P_{2,2}&\dots &P_{2,j}&\dots &P_{2,S}\\\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\P_{i,1}&P_{i,2}&\dots &P_{i,j}&\dots &P_{i,S}\\\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\P_{S,1}&P_{S,2}&\dots &P_{S,j}&\dots &P_{S,S}\\\end{matrix}}\right].}$

由于从状态 ${\displaystyle i}$ 到下一状态的概率总和必须是 1，这个矩阵是一个右随机矩阵，于是

${\displaystyle \sum _{j}P_{i,j}=1\,}$

从 ${\displaystyle i}$ 到 ${\displaystyle j}$ 分两步转变的概率由然后由给定的 ${\displaystyle P}$ 的平方矩阵的 ${\displaystyle (i,j)}$ 号元素给出：

${\displaystyle \left(P^{2}\right)_{i,j}}$

一般地，在由矩阵${\displaystyle P}$给出的有限马尔可夫链上从任何状态转移到另一个状态的 k 步转移概率为 ${\displaystyle P^{k}}$。

初始分布为一个。

平稳概率向量 ${\displaystyle {\boldsymbol {\pi }}}$ 定义为不随转移矩阵的运用而变化的一个向量；也就是说，它定义为概率矩阵的左特征向量，其特征值为1：

${\displaystyle {\boldsymbol {\pi }}P={\boldsymbol {\pi }}}$

佩龙一弗罗宾尼斯定理保证了每个随机矩阵都具有这样的向量，而特征值的最大绝对值始终为1。在一般情况下，可能有多个这样的向量。然而，对于具有严格正项的矩阵，该向量是唯一的，并可以观察到对任意 ${\displaystyle i}$ 我们都有以下极限而求出，

${\displaystyle \lim _{k\rightarrow \infty }\left(P^{k}\right)_{i,j}={\boldsymbol {\pi }}_{j}}$ ，

其中 ${\displaystyle {\boldsymbol {\pi }}_{j}}$ 是向量 ${\displaystyle {\boldsymbol {\pi }}}$ 的第 ${\displaystyle j}$ 个元素。在其他方面，这表示处在状态 ${\displaystyle j}$ 下的长期概率与初始状态 ${\displaystyle i}$ 是独立的。这两种计算得到相同的稳定向量是遍历定理的一种形式，在各种各样的耗散动力系统广泛成立：该系统随着时间演变到定态。

直观地看，随机矩阵表示一个马尔可夫链；对概率分布应用随机矩阵，就是将原始分布的概率质量进行重新分布，同时保持其总质量。如果反复应用此过程，分布就会收敛为马尔可夫链的平稳分布。

轉移矩陣可用以表示機率(或變化比率)，而矩陣相乘的結果可用以預測未來事件發生的機率。

設${\displaystyle \mathbf {A} }$、${\displaystyle \mathbf {B} }$為二個n×n階轉移矩陣，則以下亦為轉移矩陣:

• ${\displaystyle \mathbf {AB} }$
• ${\displaystyle \mathbf {A} ^{2}}$
• ${\displaystyle {\frac {1}{2}}(\mathbf {A} +\mathbf {B} )}$

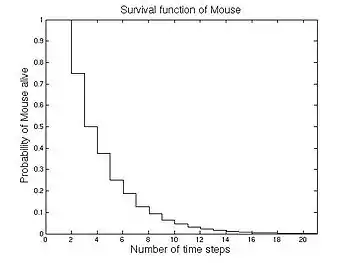
假设你有一个计时器和五个相邻的格子排成一行，零时刻有一只猫在第一个格子中，而一只老鼠在第五个格子中。在计时器增加的时候猫和老鼠都会随机跳到一个相邻的格子中。例如，如果猫在第二个格子，老鼠在第四个，在计时器增加后，猫会出现在第一个格子且老鼠会出现在第五个格子的概率为1/4。如果猫在第一个格子而老鼠在第五个，那么计时器增加后，猫会出现在第二个格子且老鼠会出现在第四个的概率为1。当它们处于同一个格子的时候，猫会吃掉老鼠，游戏结束。随机变量 K 给出了老鼠仍留在游戏中的时间步长。

表示这个包含五种位置组合 (猫,鼠) 的状态的游戏的马尔可夫链为：

• 状态 1：(1,3)
• 状态 2：(1,5)
• 状态 3：(2,4)
• 状态 4：(3,5)
• 状态 5：游戏结束：(2,2), (3,3) & (4,4)

我们使用一个随机矩阵来表示这个系统的转移概率（这个矩阵中的行和列用上面提到的可能状态来索引），

${\displaystyle P={\begin{bmatrix}0&0&1/2&0&1/2\\0&0&1&0&0\\1/4&1/4&0&1/4&1/4\\0&0&1/2&0&1/2\\0&0&0&0&1\end{bmatrix}}}$

位相型表示

老鼠的生存函数。老鼠至少在第一个时间步长存活。

由于状态 5 是一个吸收态，吸收对时间的分布为离散位相型分布。假设系统从状态 2 开始，表示为向量 ${\displaystyle [0,1,0,0,0]}$。老鼠死亡后的状态不会对生存平均产生影响，所以状态五可以忽略。初始状态和转移矩阵可以化简为，

${\displaystyle {\boldsymbol {\tau }}=[0,1,0,0]}$

以及，

${\displaystyle T={\begin{bmatrix}0&0&1/2&0\\0&0&1&0\\1/4&1/4&0&1/4\\0&0&1/2&0\end{bmatrix}}}$；而 ${\displaystyle (I-T)^{-1}{\boldsymbol {1}}={\begin{bmatrix}2.75\\4.5\\3.5\\2.75\end{bmatrix}}\,,}$

其中 ${\displaystyle I}$ 为单位矩阵，${\displaystyle \mathbf {1} }$ 表示全为1的矩阵，进行状态的相加。

由于每个状态都占据一个时间步长，老鼠生存时间的期望就是在所有生存状态和时间步长中占据的概率之和，

${\displaystyle E[K]={\boldsymbol {\tau }}(I+T+T^{2}+\cdots ){\boldsymbol {1}}={\boldsymbol {\tau }}(I-T)^{-1}{\boldsymbol {1}}=4.5}$

其高阶矩为

${\displaystyle E[K(K-1)\dots (K-n+1)]=n!{\boldsymbol {\tau }}(I-{T})^{-n}{T}^{n-1}\mathbf {1} \ }$

• Muirhead's inequality
• 佩龙一弗罗宾尼斯定理
• 密度矩陣
• 双随机矩阵
• Discrete phase-type distribution
• 概率自动机
• Models of DNA evolution
• 马尔可夫核，随机矩阵在连续状态空间的等价形式

• G. Latouche, V. Ramaswami. Introduction to Matrix Analytic Methods in Stochastic Modeling, 1st edition. Chapter 2: PH Distributions; ASA SIAM, 1999.